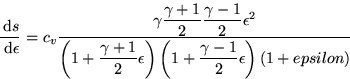...see
An interesting question is: how small is the entropy change across weak shocks precisely? That can be seen from the full equation (3'), written in terms of specific volume 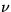$\nu$ instead of density:

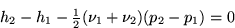
\begin{displaymath} h_2 - h_1 - {\textstyle \frac12} ( \nu_1+ \nu_2) (p_2 - p_1) = 0\end{displaymath}

In the 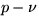$p-\nu$ plane, connect states 1 and 2 by a straight line:

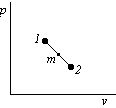
\begin{displaymath} \hbox{\epsffile{figures/4.ps}}\end{displaymath}

Note that the second term in the equation above is the trapezium rule approximation for 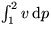$\int_1^2 v \,\mbox{d}p$, and that the trapezium rule is exact for a linear function. So along this straight connecting line

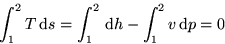
\begin{displaymath} \int_1^2 T\,\mbox{d}s = \int_1^2 \,\mbox{d}h - \int_1^2 v \,\mbox{d}p = 0 \end{displaymath}

exactly. Now approximate the left integral with the midpoint rule:

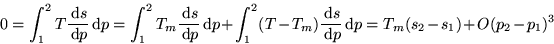
\begin{displaymath} 0 = \int_1^2 T\frac{\,\mbox{d}s}{\,\mbox{d}p}\,\mbox{d}p = ... ...ox{d}s}{\,\mbox{d}p}\,\mbox{d}p = T_m (s_2-s_1) + O(p_2-p_1)^3\end{displaymath}

where m is the mid point between 1 and 2 in the 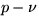$p-\nu$ diagram. It follows that the entropy change across a weak shock is very small, proportional to the cube of the already small pressure difference. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...grey.
The discussion above is a bit simplistic, since there are two thermodynamic variables plus a velocity to approximate: in reality you will need to approximate all three at the same time using shocks moving left with the speed of sound, shocks moving right with the speed of sound, and jumps that remain stationary compared to the gas. The third set of jumps are called ``contact discontinuities'', rather than shocks. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...entropy
This is a pain. To do it, write (8a) and (8b) in terms of the Mach number, M1*, write 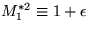$M_1^{*2}\equiv1+\epsilon$,plug in the equation for the entropy,

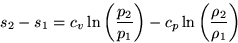
\begin{displaymath} s_2 - s_1 = c_v \ln\left(\frac{p_2}{p_1}\right) - c_p \ln\left(\frac{\rho_2}{\rho_1}\right)\end{displaymath}

and take the derivative w.r.t. 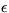$\epsilon$ to get:

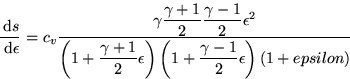
\begin{displaymath} \frac{\,\mbox{d}s}{\,\mbox{d}\epsilon} = c_v \frac{\gamma{\... ...ystyle\frac{\gamma-1}2}\epsilon\right) \left(1+epsilon\right)}\end{displaymath}

Which is always positive, so the entropy increase becomes positive for 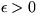$\epsilon\gt$, i.e. M1*>1. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.