Next: Conserved stagnation enthalpy
Up: Governing Equations
Previous: Governing Equations
The configuration we look at for a normal shock is shown once more:
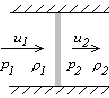
The question now is: given the gas and the state 1 before the shock,
what are the flow variables u2, p2, and 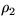 behind the
shock?
behind the
shock?
To answer the question, i.e. compute the three variables, we need three
equations. They are:
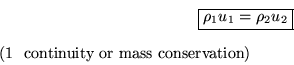
This equation simply says that the mass that is flowing into the shock
at side 1 per unit time and per unit shock area is also the mass flowing
out of the shock at side 2.
Next, the equation
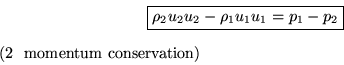
says that the increase of linear momentum flowing out at
2 compared to the linear momentum flowing in at 1 is according to
Newton's second law equal to the net pressure force on the fluid. (All
per unit shock area.) Note that we are ignoring viscous shear forces on
the top and bottom ends of the shock, which is OK, for one reason since the
shock is thin. (Another reason: if the state of the shock at its top
and bottom ends is the same, Newton's law of action being opposite
to reaction implies that the shear forces will cancel each other.)
The third equation is conservation of energy. It is our familiar
relationship:
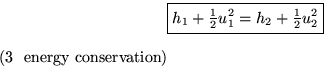
It says that internal energy flowing in plus work being done by the
pressure at inflow (both included in the enthalpy h) plus kinetic
energy flowing in equals internal energy flowing out, work being done
by the pressure at outflow, and kinetic energy flowing out. (All
per unit mass flowing through.)
Before starting to grind down those equations, let's first look at
them, OK?
First of all, there are three equations in three unknowns, 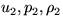 ,which seems just fine. Do note that one ``solution'' is the trivial
one,
,which seems just fine. Do note that one ``solution'' is the trivial
one, 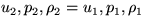 ,where there is no shock and the flow quantities at 2 are exactly
the same as at 1. (You can easily check that this satisfies all three
conservation equations above.) But the equations are nonlinear, so
there may be another solution. (For example, you know that
a simple quadratic equation has two roots.)
,where there is no shock and the flow quantities at 2 are exactly
the same as at 1. (You can easily check that this satisfies all three
conservation equations above.) But the equations are nonlinear, so
there may be another solution. (For example, you know that
a simple quadratic equation has two roots.)
So let's see what we can say apriori about any nontrivial solutions.
Next: Conserved stagnation enthalpy
Up: Governing Equations
Previous: Governing Equations
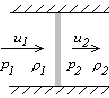
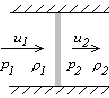
![]() behind the
shock?
behind the
shock?
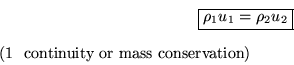
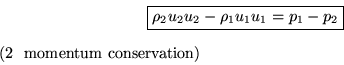
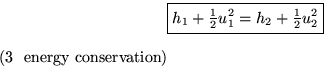
![]() ,which seems just fine. Do note that one ``solution'' is the trivial
one,
,which seems just fine. Do note that one ``solution'' is the trivial
one, ![]() ,where there is no shock and the flow quantities at 2 are exactly
the same as at 1. (You can easily check that this satisfies all three
conservation equations above.) But the equations are nonlinear, so
there may be another solution. (For example, you know that
a simple quadratic equation has two roots.)
,where there is no shock and the flow quantities at 2 are exactly
the same as at 1. (You can easily check that this satisfies all three
conservation equations above.) But the equations are nonlinear, so
there may be another solution. (For example, you know that
a simple quadratic equation has two roots.)