|
|
|
|
Skip to: 2.1.2 More on delta and Green’s functions |
|
Show that
Answer:
First of all, define a second anti-derivative of ![]() to be
to be ![]() . That allows you from now on to write
. That allows you from now on to write ![]() as
as ![]() . Note also that
. Note also that ![]() is one possible solution to the Poisson equation.
is one possible solution to the Poisson equation.
Now restrict the region of integration of ![]() to
to ![]() where
where ![]() is some large number. (You can take the limit
is some large number. (You can take the limit ![]() at the end of the story.)
at the end of the story.)
Split the integral into two parts ![]() and
and ![]() because the absolute value in the integral is different in these two cases. You get
because the absolute value in the integral is different in these two cases. You get
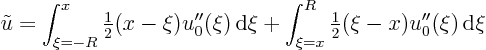
You then find that ![]() is indeed a solution to the Poisson equation.
is indeed a solution to the Poisson equation.