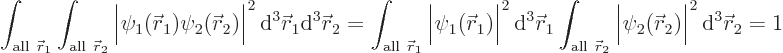5.1.1 So­lu­tion com­plex-a

Ques­tion:

A sim­ple form that a six-di­men­sion­al wave func­tion can take is a prod­uct of two three-di­men­sion­al ones, as in $\psi({\skew0\vec r}_1,{\skew0\vec r}_2)$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\psi_1({\skew0\vec r}_1)\psi_2({\skew0\vec r}_2)$. Show that if $\psi_1$ and $\psi_2$ are nor­mal­ized, then so is $\psi$.

An­swer:

This is a di­rect con­se­quence of the fact that in­te­grals can be fac­tored if their in­te­grands can be and the lim­its of in­te­gra­tion are in­de­pen­dent of the other vari­able:

$$\int_{{\rm all }{\skew0\vec r}_1}\int_{{\rm all }{\skew0\v... ...({\skew0\vec r}_2)\Big\vert^2 { \rm d}^3 {\skew0\vec r}_2 = 1$$