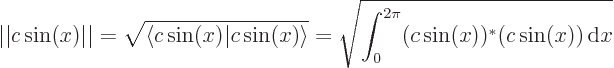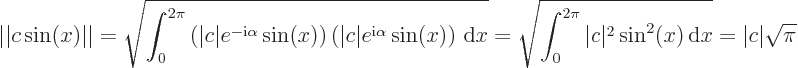| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
2.3.6 Solution dot-f
Question:
Verify that the most general multiple of 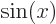 that is normalized on the interval 0
that is normalized on the interval 0 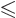
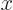
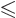
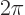 is
is 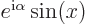
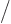
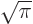 where
where 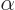 is any arbitrary real number. So, using the Euler formula, the following multiples of
is any arbitrary real number. So, using the Euler formula, the following multiples of 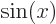 are all normalized:
are all normalized: 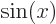
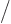
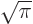 , (for
, (for 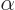
 0),
0), 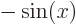
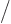
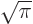 , (for
, (for 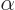

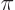 ), and
), and 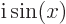
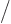
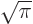 , (for
, (for 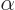

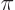
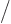 2).
2).
Answer:
A multiple of 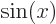 means
means 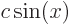 , where
, where 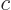 is some complex constant, so the magnitude is
is some complex constant, so the magnitude is
You can always write 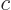 as
as 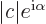 where
where 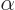 is some real angle, and then you get for the norm:
is some real angle, and then you get for the norm:
So for the multiple to be normalized, the magnitude of 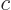 must be
must be 
 1/
1/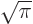 , but the angle
, but the angle 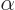 can be arbitrary.
can be arbitrary.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() )
)![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()