| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
4.4.2.1 Solution esdb-a
Question:
The 2p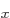 pointer state of the hydrogen atom was defined as
pointer state of the hydrogen atom was defined as
What are the expectation values of energy, square angular momentum, and  angular momentum for this state?
angular momentum for this state?
Answer:
Note that the square coefficients of the eigenfunctions 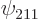 and
and 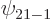 are each
are each 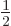 , so each has a probability
, so each has a probability 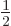 in the 2p
in the 2p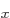 state.
state.
Eigenfunction 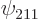 has an energy eigenvalue
has an energy eigenvalue 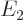 , and so does
, and so does 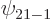 , so the expectation value of energy in the 2p
, so the expectation value of energy in the 2p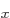 state is
state is
This is as expected since the only value that can be measured in this state is 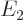 .
.
Similarly, eigenfunction 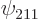 has a square angular momentum eigenvalue
has a square angular momentum eigenvalue 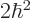 , and so does
, and so does 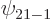 , so the expectation value of square angular momentum in the 2p
, so the expectation value of square angular momentum in the 2p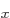 state is that value,
state is that value,
Eigenfunction 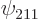 has a
has a  angular momentum eigenvalue
angular momentum eigenvalue 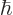 , and
, and 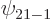 has
has 
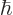 , so the expectation value of
, so the expectation value of  angular momentum in the 2p
angular momentum in the 2p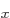 state is
state is
Measurements in which the  angular momentum is found to be
angular momentum is found to be 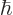 average out against those where it is found to be
average out against those where it is found to be 
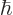 .
.
![]()
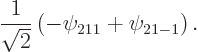
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() ,
,![]() ,
,![]()
![]()
![]() ,
,![]() ,
,![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()