| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
4.1.3.2 Solution harmc-b
Question:
Verify that there are no sets of quantum numbers missing in the spectrum figure 4.1; the listed ones are the only ones that produce those energy levels.
Answer:
The generic expression for the energy is
or defining 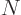

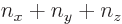 ,
,
Now for the bottom level, 
 0, and since the three quantum numbers
0, and since the three quantum numbers 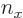 ,
, 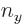 , and
, and 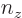 cannot be negative, the only way that
cannot be negative, the only way that 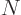

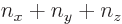 can be zero is if all three numbers are zero. If any one of
can be zero is if all three numbers are zero. If any one of 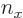 ,
, 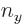 , or
, or 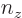 would be positive, then so would be
would be positive, then so would be 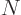 . So there is only one state
. So there is only one state 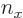

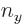

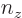
 0.
0.
For the second energy level, 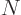
 1. To get a nonzero sum
1. To get a nonzero sum 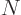 , you must have one of
, you must have one of 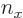 ,
, 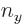 , and
, and 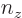 to be nonzero, but not more than 1, or
to be nonzero, but not more than 1, or 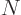 would be more than 1 too. Also, if one of
would be more than 1 too. Also, if one of 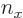 ,
, 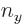 , and
, and 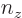 is 1, then the other two must be 0 or their sum
is 1, then the other two must be 0 or their sum 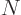 would still be greater than 1. That means that precisely one of
would still be greater than 1. That means that precisely one of 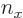 ,
, 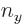 , and
, and 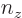 must be 1 and the other two 0. There are three possibilities for the one that is 1,
must be 1 and the other two 0. There are three possibilities for the one that is 1, 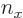 ,
, 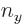 , or
, or 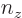 , resulting in the three different sets of quantum numbers shown in the spectrum figure 4.1.
, resulting in the three different sets of quantum numbers shown in the spectrum figure 4.1.
For the third energy level, 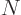
 2, the maximum value value any one of
2, the maximum value value any one of 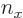 ,
, 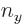 , and
, and 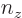 could possibly have is 2, but then the other two must be zero. That leads to the first three sets of quantum numbers shown in the spectrum. If the maximum value among
could possibly have is 2, but then the other two must be zero. That leads to the first three sets of quantum numbers shown in the spectrum. If the maximum value among 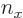 ,
, 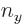 , and
, and 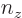 is not 2 but 1, then a second one must also be 1, or they would not add up to 2. So in this case you have two of them 1 and the third 0. There are three possibilities for the one that is 0, producing the last three sets of quantum numbers shown in the spectrum 4.1 at this energy level.
is not 2 but 1, then a second one must also be 1, or they would not add up to 2. So in this case you have two of them 1 and the third 0. There are three possibilities for the one that is 0, producing the last three sets of quantum numbers shown in the spectrum 4.1 at this energy level.
For the fourth energy level, 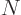
 3, the maximum value value that any one of
3, the maximum value value that any one of 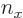 ,
, 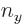 , and
, and 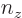 could have is 3, with the other two 0, producing the first three sets of quantum numbers. If the maximum value is 2, then the other two quantum numbers must add up to 1, which means one of them is 1 and the other 0. There are three possibilities for which quantum number is 2, and for each of these there are two possibilities for which of the other two is 1. That produces the next six sets of quantum numbers. Finally, if the maximum value is 1, then both other numbers will have to be 1 too to add up to
could have is 3, with the other two 0, producing the first three sets of quantum numbers. If the maximum value is 2, then the other two quantum numbers must add up to 1, which means one of them is 1 and the other 0. There are three possibilities for which quantum number is 2, and for each of these there are two possibilities for which of the other two is 1. That produces the next six sets of quantum numbers. Finally, if the maximum value is 1, then both other numbers will have to be 1 too to add up to 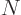
 3. That gives the tenth set.
3. That gives the tenth set.
A less intuitive, but more general, procedure is to simply derive the number of different eigenstates 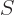 for a given
for a given 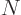 mathematically and show that it agrees with the figure: The possible values that the quantum number
mathematically and show that it agrees with the figure: The possible values that the quantum number 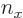 can have in order for
can have in order for 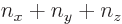 not to exceed
not to exceed 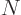 are in the range from 0 to
are in the range from 0 to 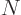 , and for each such value of
, and for each such value of 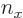 ,
, 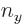 must be in the range from 0 to
must be in the range from 0 to 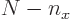 for
for 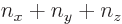 no to exceed
no to exceed 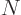 . For each such acceptable pair of values
. For each such acceptable pair of values 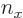 and
and 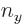 , there is exactly one allowed value
, there is exactly one allowed value 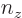

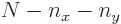 . So there is exactly one state for each acceptable pair of values
. So there is exactly one state for each acceptable pair of values 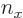 and
and 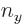 . Which means that the number of states is, using summation symbols,
. Which means that the number of states is, using summation symbols,
The sum within the parentheses is 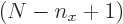
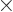 1, and then the remaining sum is an arithmetic series [1, 21.1], producing
1, and then the remaining sum is an arithmetic series [1, 21.1], producing
Substituting in 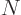
 0, you get
0, you get 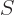
 1, a single state, for
1, a single state, for 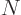
 1,
1, 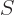
 3, three states, for
3, three states, for 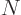
 2 six states and for
2 six states and for 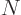
 3 ten states. So the spectrum 4.1 shows all states.
3 ten states. So the spectrum 4.1 shows all states.
![]()
![]()
![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
![]() ,
,![]() ,
,![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() ,
,![]() ,
,![]()
![]()
![]() ,
,![]() ,
,![]()
![]()
![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,![]()
![]()
![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]()
![]()
![]()
![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() ,
,![]()
![]()
![]()
![]() .
.![]()
![]() ,
,![]()
![]()
![]() .
.![]()
![]() .
.