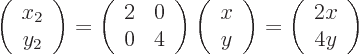| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
2.6.1 Solution herm-a
Question:
A matrix 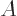 is defined to convert any vector
is defined to convert any vector 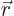

 into
into 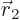

 . Verify that
. Verify that 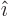 and
and 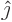 are orthonormal eigenvectors of this matrix, with eigenvalues 2, respectively 4.
are orthonormal eigenvectors of this matrix, with eigenvalues 2, respectively 4.
Answer:
Take 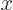
 1,
1, 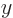
 0 to get that
0 to get that 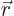

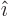 transforms into
transforms into 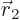

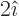 . Therefore
. Therefore 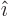 is an eigenvector, and the eigenvalue is 2. The same way, take
is an eigenvector, and the eigenvalue is 2. The same way, take 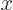
 0,
0, 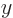
 1 to get that
1 to get that 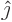 transforms into
transforms into 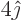 , so
, so 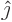 is an eigenvector with eigenvalue 4. The vectors
is an eigenvector with eigenvalue 4. The vectors 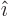 and
and 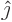 are also orthogonal and of length 1, so they are orthonormal.
are also orthogonal and of length 1, so they are orthonormal.
In linear algebra, you would write the relationship 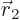

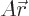 out as:
out as:
In short, vectors are represented by columns of numbers and matrices by square tables of numbers.
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()