| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
2.6.7 Solution herm-g
Question:
Show that if 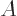 is a Hermitian operator, then so is
is a Hermitian operator, then so is 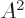 . As a result, under the conditions of the previous question,
. As a result, under the conditions of the previous question, 
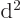
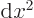 is a Hermitian operator too. (And so is just
is a Hermitian operator too. (And so is just 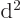
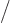
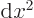 , of course, but
, of course, but 
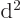
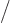
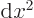 is the one with the positive eigenvalues, the squares of the eigenvalues of
is the one with the positive eigenvalues, the squares of the eigenvalues of 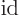
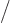
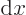 .)
.)
Answer:
To show that 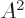 is Hermitian, just move the two operators
is Hermitian, just move the two operators 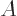 to the other side of the inner product one by one. As far as the eigenvalues are concerned, each application of
to the other side of the inner product one by one. As far as the eigenvalues are concerned, each application of 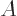 to one of its eigenfunctions multiplies by the eigenvalue, so two applications of
to one of its eigenfunctions multiplies by the eigenvalue, so two applications of 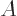 multiplies by the square eigenvalue.
multiplies by the square eigenvalue.
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()