| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
4.6.6.1 Solution hione-a
Question:
The solution for the hydrogen molecular ion requires elaborate evaluations of inner product integrals and a computer evaluation of the state of lowest energy. As a much simpler example, you can try out the variational method on the one-dimensional case of a particle stuck inside a pipe, as discussed in chapter 3.5. Take the approximate wave function to be:
Find 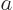 from the normalization requirement that the total probability of finding the particle integrated over all possible
from the normalization requirement that the total probability of finding the particle integrated over all possible 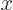 positions is one. Then evaluate the energy
positions is one. Then evaluate the energy 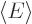 as
as 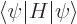 , where according to chapter 3.5.3, the Hamiltonian is
, where according to chapter 3.5.3, the Hamiltonian is
Compare the ground state energy with the exact value,
(Hints: 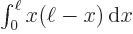

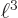
 6 and
6 and 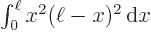

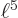
 30)
30)
Answer:
To satisfy the normalization requirement that the particle must be somewhere, you need 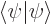
 1, or substituting for
1, or substituting for 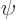 ,
,
And by definition, chapter 2.3, the final inner product is just the integral 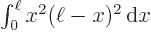 which is given to be
which is given to be 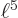
 30. So you must have
30. So you must have
Now evaluate the expectation energy:
You can substitute in the value of  from the normalization requirement above and apply the Hamiltonian on the function to its right:
from the normalization requirement above and apply the Hamiltonian on the function to its right:
The inner product is by definition the integral 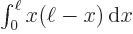 , which was given to be
, which was given to be 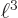
 6. So the final expectation energy is
6. So the final expectation energy is
The error in the approximation is only 1.3%! That is a surprisingly good result, since the parabola 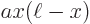 and the sine
and the sine 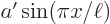 are simply different functions. While they may have superficial resemblance, if you scale each to unit height by taking
are simply different functions. While they may have superficial resemblance, if you scale each to unit height by taking 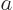
 4
4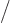
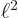 and
and 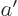
 1, then the derivatives at
1, then the derivatives at 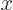
 0 and
0 and 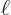 are 4
are 4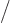
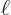 respectively
respectively 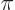
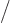
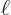 , off by as much as 27%.
, off by as much as 27%.
If you go the next logical step, approximating the ground state with two functions as
where 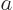 and
and 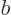 are related by the normalization requirement
are related by the normalization requirement 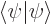
 1, you find a ground state energy to a stunning, (for a two term approximation,) accuracy of 0.001 5%! However, the algebra becomes impossibly messy, so it was left out of the questions list. Similarly, a two point, linear interpolation, finite element version was left out, since there is so much baggage, it would distract from the true purpose of this book, to bring across the basic ideas of quantum mechanics to engineers.
1, you find a ground state energy to a stunning, (for a two term approximation,) accuracy of 0.001 5%! However, the algebra becomes impossibly messy, so it was left out of the questions list. Similarly, a two point, linear interpolation, finite element version was left out, since there is so much baggage, it would distract from the true purpose of this book, to bring across the basic ideas of quantum mechanics to engineers.
Now, if you read the next subsection, you will see that in real-life, multi-dimensional, problems, getting results this accurate is difficult. Still, if you are desperate for a good solution of these very complex problems by a simple and reliable means, variational methods are hard to beat.
![]()
![]()
![]() ,
,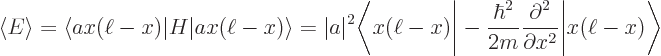
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,