| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
4.3.4.2 Solution hydd-b
Question:
Check from the conditions
that 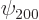 ,
, 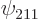 ,
, 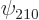 , and
, and 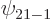 are the only states of the form
are the only states of the form 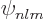 that have energy
that have energy 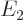 . (Of course, all their combinations, like 2p
. (Of course, all their combinations, like 2p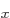 and 2p
and 2p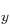 , have energy
, have energy 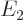 too, but they are not simply of the form
too, but they are not simply of the form 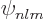 , but combinations of the
, but combinations of the basic
solutions 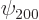 ,
, 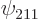 ,
, 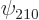 , and
, and 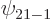 .)
.)
Answer:
Since the energy is given to be 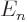

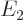 , you have
, you have 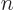
 2. The azimuthal quantum number
2. The azimuthal quantum number 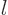 must be a smaller nonnegative integer, so it can only be 0 or 1. In case
must be a smaller nonnegative integer, so it can only be 0 or 1. In case 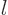
 0, the absolute value of the magnetic quantum number
0, the absolute value of the magnetic quantum number 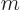 cannot be more than zero, allowing only
cannot be more than zero, allowing only 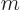
 0. That is the
0. That is the 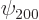 state. In the case that
state. In the case that 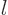
 1, the absolute value of
1, the absolute value of 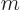 can be up to one, allowing
can be up to one, allowing 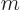
 1, 0, and
1, 0, and  1.
1.
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 1
1