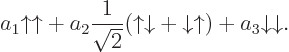5.6.1 So­lu­tion ident-a

Ques­tion:

Check that in­deed any lin­ear com­bi­na­tion of the triplet states is un­changed un­der par­ti­cle ex­change.

An­swer:

In the no­ta­tions of the pre­vi­ous sec­tion, the most gen­eral lin­ear com­bi­na­tion of the triplet states takes the form:

$$a_1 {\left\vert 1\:1\right\rangle} + a_2 {\left\vert 1\:0\ri... ...le} + a_3{\left\vert 1\:\rule[2.5pt]{5pt}{.5pt}1\right\rangle}$$

or writ­ing out their de­f­i­n­i­tions as found there,

$$a_1 {\uparrow}{\uparrow}+ a_2 \frac{1}{\sqrt{2}}({\uparrow}{... ...arrow}+{\downarrow}{\uparrow}) + a_3 {\downarrow}{\downarrow}.$$

Ex­chang­ing the two par­ti­cles in­volved means to in­ter­change the or­der of each pair of ar­rows, since by de­f­i­n­i­tion the first ar­row refers to par­ti­cle 1 and the sec­ond to par­ti­cle 2. A look at the ex­pres­sion above shows that such an in­ter­change of or­der does ab­solutely noth­ing to these states.