| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
2.4.4 Solution mathops-d
Question:
The inversion, or parity, operator 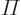 turns
turns 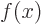 into
into 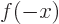 . (It plays a part in the question to what extent physics looks the same when seen in the mirror.) Show that
. (It plays a part in the question to what extent physics looks the same when seen in the mirror.) Show that  leaves
leaves 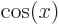 unchanged, but turns
unchanged, but turns 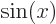 into
into 
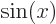 .
.
Answer:
According to [1, p. 43], 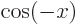

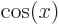 , but
, but 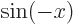


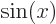 . Compare also the graphs of the functions on the same page;
. Compare also the graphs of the functions on the same page; 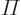 flips the graph of a function over around the
flips the graph of a function over around the  -axis.
-axis.
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() .
.![]()
![]() -
-