| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
3.5.6.2 Solution pipee-b
Question:
Just for fun, plug macroscopic values, 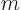
 1 kg and
1 kg and 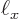
 1 m, into the expression for the ground state energy and see how big it is. Note that
1 m, into the expression for the ground state energy and see how big it is. Note that 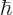
 1.054 57 10
1.054 57 10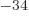 J s.
J s.
Answer:
or 3.4 10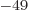 eV. That energy is much less than you could ever hope to observe physically. A single photon of light would dwarf it by 50 orders of magnitude.
eV. That energy is much less than you could ever hope to observe physically. A single photon of light would dwarf it by 50 orders of magnitude.
![]()
![]()
![]()
![]()
![]()
![]()
![]()