3.5.7.3 So­lu­tion pipef-c

Ques­tion:

If you are up to a trick ques­tion, con­sider the fol­low­ing. There are no forces in­side the pipe, so the par­ti­cle has to keep mov­ing un­til it hits an end of the pipe, then re­flect back­ward un­til it hits the other side and so on. So, it has to cross the cen­ter of the pipe reg­u­larly. But in the en­ergy eigen­state 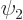$\psi_2$, the par­ti­cle has zero chance of ever be­ing found at the cen­ter of the pipe. What gives?

An­swer:

Al­most every word in the above story is a gross mis­state­ment of what na­ture re­ally is like when ex­am­ined on quan­tum scales. A par­ti­cle does not have a po­si­tion, so phrases like hits an end”, re­flect back­ward, and “keep mov­ing are truly mean­ing­less. On macro­scopic scales a par­ti­cle may have an rel­a­tively pre­cisely de­fined po­si­tion, but that is only be­cause there is un­cer­tainty in en­ergy. If you could bring a macro­scopic par­ti­cle truly into a sin­gle en­ergy eigen­state, it too would have no po­si­tion. And the small­est thing you might do to fig­ure out where it is would kick it out of that sin­gle en­ergy state.