| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
3.5.8.3 Solution pipeg-c
Question:
Shade the regions where the particle is likely to be found in the 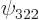 energy eigenstate.
energy eigenstate.
Answer:
The wave function is
Now the trick is to realize that the wave function is zero when any of the three sines is zero. Looking along the  -direction, you will see an array of 3 times 2 blobs, or 6 blobs:
-direction, you will see an array of 3 times 2 blobs, or 6 blobs:
Figure 3.2:
Eigenstate 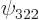 .
.
![\begin{figure}\centering {}
\setlength{\unitlength}{1pt}
\begin{picture}(451,12...
...0,0)[l]{light}}
\put(-130,4){\makebox(0,0)[l]{light}}
\end{picture}
\end{figure}](img226.gif) |
The white horizontal centerline line along the pipe corresponds to 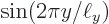 being zero at
being zero at 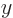

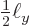 , and the two white vertical white lines correspond to
, and the two white vertical white lines correspond to 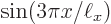 being zero at
being zero at 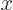

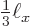 and
and 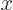

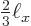 . The
. The 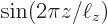 factor in the wave function will split it further into six blobs front and 6 blobs rear, but that is not visible when looking along the
factor in the wave function will split it further into six blobs front and 6 blobs rear, but that is not visible when looking along the  -direction; the front blobs cover the rear ones. Seen from the top, you would again see an array of 3 times 2 blobs, the top blobs hiding the bottom ones.
-direction; the front blobs cover the rear ones. Seen from the top, you would again see an array of 3 times 2 blobs, the top blobs hiding the bottom ones.
![]()
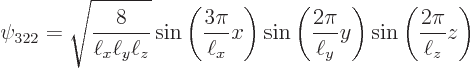
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]() -
-