A.28.1 So­lu­tion wkb-a

Ques­tion:

Use the equa­tion

$$\frac{1}{\hbar} \int_{{\underline x}=x_1}^{x_2} p_{\rm {c}}({\underline x}) { \rm d}{\underline x}= n \pi$$

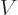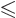
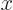
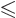
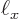
to find the WKB ap­prox­i­ma­tion for the en­ergy lev­els of a par­ti­cle stuck in a pipe of chap­ter 3.5.5. The po­ten­tial $V$ is zero in­side the pipe, given by 0 $\raisebox{-.3pt}{$\leqslant$}$ $x$ $\raisebox{-.3pt}{$\leqslant$}$ $\ell_x$

In this case, the WKB ap­prox­i­ma­tion pro­duces the ex­act re­sult, since the clas­si­cal mo­men­tum re­ally is con­stant. If there was a force field in the pipe, the so­lu­tion would only be ap­prox­i­mate.

An­swer:

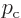
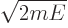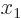
Sub­sti­tut­ing in $p_{\rm {c}}$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\sqrt{2mE}$, $x_1$ $\vphantom0\raisebox{1.5pt}{$=$}$ 0 and $x_2$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\ell_x$,

$$\frac{1}{\hbar} \sqrt{2mE} \ell_x = n \pi$$

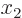
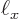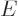
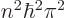
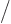
and squar­ing both sides, the en­ergy is found as 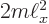$E$ $\vphantom0\raisebox{1.5pt}{$=$}$ $n^2\hbar^2\pi^2$$\raisebox{.5pt}{$/$}$​$2m\ell_x^2$. That is the same re­sult as in chap­ter 3.5.5, but ob­tained in a much eas­ier way.
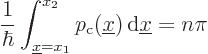