| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
12.1 Introduction
The standard eigenfunctions of orbital angular momentum are the so
called spherical harmonics
of chapter 4.2.
They show that the square orbital angular momentum has the possible
values
The nonnegative integer 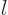 is called the azimuthal quantum number.
is called the azimuthal quantum number.
Further, the orbital angular momentum in any arbitrarily chosen
direction, taken as the 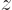 -direction from now on, comes in multiples
-direction from now on, comes in multiples
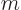 of Planck's constant
of Planck's constant 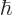 :
:
The integer 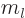 is called the magnetic quantum number.
is called the magnetic quantum number.
The possible values of the square spin angular momentum can be
written as
The spin azimuthal quantum number
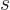 is usually
called the
is usually
called the spin
for short. Note that while the
orbital azimuthal quantum number 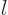 had to be an integer, the spin
can be half integer. But one important conclusion of this chapter
will be that the spin cannot be anything more. A particle with, say,
spin
had to be an integer, the spin
can be half integer. But one important conclusion of this chapter
will be that the spin cannot be anything more. A particle with, say,
spin 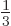 cannot not exist according to the theory.
cannot not exist according to the theory.
For the spin angular momentum in the 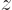 -direction
-direction
Note that if the spin 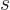 is half integer, then so are all the spin
magnetic quantum numbers
is half integer, then so are all the spin
magnetic quantum numbers 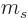 . If the nature of the angular
momentum is self-evident, the subscript
. If the nature of the angular
momentum is self-evident, the subscript 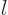 or
or 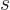 of the magnetic
quantum numbers
of the magnetic
quantum numbers 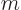 will be omitted.
will be omitted.
Particles with half-integer spin are called fermions. That includes
electrons, as well as protons and neutrons and their constituent
quarks. All of these critically important particles have spin
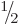 . (Excited proton and neutron states can have spin
. (Excited proton and neutron states can have spin
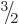 .) Particles with integer spin are bosons. That
includes the particles that act as carriers of fundamental forces; the
photons, intermediate vector bosons, gluons, and gravitons. All of
these have spin 1, except the graviton which supposedly has spin 2.
.) Particles with integer spin are bosons. That
includes the particles that act as carriers of fundamental forces; the
photons, intermediate vector bosons, gluons, and gravitons. All of
these have spin 1, except the graviton which supposedly has spin 2.
![]() -
-![]()
![]() :
:![]() -
-![]() .
.![]() .
.