| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
13.1 The Electromagnetic Hamiltonian
This section describes very basically how electromagnetism fits into
quantum mechanics. However, electromagnetism is fundamentally
relativistic; its carrier, the photon, readily emerges or disappears.
To describe electromagnetic effects fully requires quantum
electrodynamics, and that is far beyond the scope of this text.
(However, see addenda {A.15} and {A.23} for
some of the ideas.)
In classical electromagnetics, the force on a particle with charge 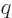 in a field with electric strength
in a field with electric strength 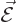 and magnetic strength
and magnetic strength 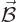 is given by the Lorentz force law
is given by the Lorentz force law
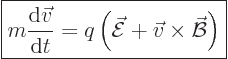 |
(13.1) |
where 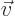 is the velocity of the particle and for an electron,
the charge is
is the velocity of the particle and for an electron,
the charge is 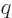


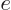 .
.
Unfortunately, quantum mechanics uses neither forces nor velocities.
In fact, the earlier analysis of atoms and molecules in this book used
the fact that the electric field is described by the corresponding
potential energy 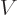 , see for example the Hamiltonian of the
hydrogen atom. The magnetic field must appear differently in the
Hamiltonian; as the Lorentz force law shows, it couples with velocity.
You would expect that still the Hamiltonian would be relatively
simple, and the simplest idea is then that any potential corresponding
to the magnetic field moves in together with momentum. Since the
momentum is a vector quantity, then so must be the magnetic potential.
So, your simplest guess would be that the Hamiltonian takes the form
, see for example the Hamiltonian of the
hydrogen atom. The magnetic field must appear differently in the
Hamiltonian; as the Lorentz force law shows, it couples with velocity.
You would expect that still the Hamiltonian would be relatively
simple, and the simplest idea is then that any potential corresponding
to the magnetic field moves in together with momentum. Since the
momentum is a vector quantity, then so must be the magnetic potential.
So, your simplest guess would be that the Hamiltonian takes the form
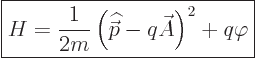 |
(13.2) |
where 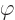

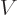

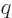 is the
is the electric potential
and
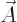 is the
is the magnetic vector potential.
And this
simplest guess is in fact right.
The relationship between the vector potential 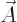 and the magnetic
field strength
and the magnetic
field strength 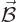 will now be found from requiring that the
classical Lorentz force law is obtained in the classical limit that
the quantum uncertainties in position and momentum are small. In that
case, expectation values can be used to describe position and
velocity, and the field strengths
will now be found from requiring that the
classical Lorentz force law is obtained in the classical limit that
the quantum uncertainties in position and momentum are small. In that
case, expectation values can be used to describe position and
velocity, and the field strengths 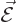 and
and 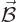 will be constant on
the small quantum scales. That means that the derivatives of
will be constant on
the small quantum scales. That means that the derivatives of
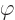 will be constant, (since
will be constant, (since 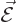 is the negative gradient of
is the negative gradient of
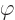 ), and presumably the same for the derivatives of
), and presumably the same for the derivatives of
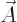 .
.
Now according to chapter 7.2, the evolution of the
expectation value of position is found as
Working out the commutator with the Hamiltonian above,
{D.71}, you get,
This is unexpected; it shows that 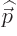 ,
i.e.
,
i.e. 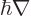

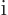 , is no longer the operator of the
normal momentum
, is no longer the operator of the
normal momentum 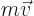 when there is a magnetic field;
when there is a magnetic field; 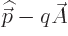 gives the normal momentum. The momentum represented by
gives the normal momentum. The momentum represented by 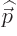 by
itself is called “canonical” momentum to distinguish it from normal momentum:
by
itself is called “canonical” momentum to distinguish it from normal momentum:
The canonical momentum 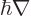

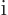 only corresponds to normal
momentum if there is no magnetic field involved.
only corresponds to normal
momentum if there is no magnetic field involved.
(Actually, it was not that unexpected to physicists, since the same
happens in the classical description of electromagnetics using the
so-called Lagrangian approach, chapter 1.3.2.)
Next, Newton’s second law says that the time derivative of the
linear momentum 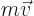 is the force. Since according to the
above, the linear momentum operator is
is the force. Since according to the
above, the linear momentum operator is 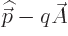 , then
, then
The objective is now to ensure that the right hand side is the correct
Lorentz force (13.1) for the assumed Hamiltonian, by a
suitable definition of 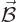 in terms of
in terms of 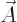 .
.
After a lot of grinding down commutators, {D.71},
it turns out that indeed the Lorentz force is obtained,
provided that:
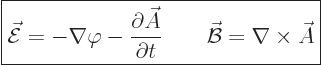 |
(13.3) |
So the magnetic field is found as the curl of the vector potential
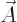 . And the electric field is no longer just the negative
gradient of the scalar potential
. And the electric field is no longer just the negative
gradient of the scalar potential 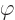 if the vector potential
varies with time.
if the vector potential
varies with time.
These results are not new. The electric scalar potential 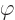 and
the magnetic vector potential
and
the magnetic vector potential 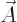 are the same in classical
physics, though they are a lot less easy to guess than done here.
Moreover, in classical physics they are just convenient mathematical
quantities to simplify analysis. In quantum mechanics they appear as
central to the formulation.
are the same in classical
physics, though they are a lot less easy to guess than done here.
Moreover, in classical physics they are just convenient mathematical
quantities to simplify analysis. In quantum mechanics they appear as
central to the formulation.
And it can make a difference. Suppose you do an experiment where
you pass electron wave functions around both sides of a very thin
magnet: you will get a wave interference pattern behind the magnet.
The classical expectation is that this interference pattern will be
independent of the magnet strength: the magnetic field 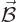 outside a
very thin and long ideal magnet is zero, so there is no force on the
electron. But the magnetic vector potential
outside a
very thin and long ideal magnet is zero, so there is no force on the
electron. But the magnetic vector potential 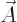 is not zero
outside the magnet, and Aharonov and Bohm argued that the interference pattern would
therefore change with magnet strength. So it turned out to be in
experiments done subsequently. The conclusion is clear; nature
really goes by the vector potential
is not zero
outside the magnet, and Aharonov and Bohm argued that the interference pattern would
therefore change with magnet strength. So it turned out to be in
experiments done subsequently. The conclusion is clear; nature
really goes by the vector potential 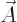 and not the magnetic field
and not the magnetic field
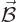 in its actual workings.
in its actual workings.
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]() )
)![]() .
.![\begin{displaymath}
\frac{{\rm d}\langle {\skew 2\widehat{\skew{-1}\vec r}}\ran...
...\langle \frac{{\rm i}}{\hbar} [H,{\skew0\vec r}] \right\rangle
\end{displaymath}](img2814.gif)
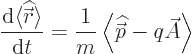
![]()
![]() ,
,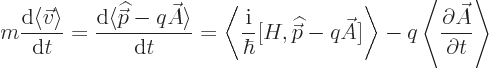
![]()
![]()
![]()
![]()
![]()
![]()