| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.63 Angular momentum uncertainty
Suppose that an eigenstate, call it 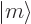 , of
, of
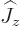 is also an eigenstate of
is also an eigenstate of 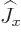 . Then
. Then
![$[{\widehat J}_z,{\widehat J}_x]\big\vert m\big\rangle$](img7297.gif) must be zero, and the commutator
relations say that this is equivalent to
must be zero, and the commutator
relations say that this is equivalent to 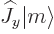
 0, which makes
0, which makes 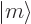 also an eigenvector of
also an eigenvector of
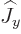 , and with the eigenvalue zero to boot. So the angular
momentum in the
, and with the eigenvalue zero to boot. So the angular
momentum in the 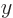 -direction must be zero. Repeating the same
argument using the
-direction must be zero. Repeating the same
argument using the ![$[{\widehat J}_x,{\widehat J}_y]$](img2680.gif) and
and ![$[{\widehat J}_y,{\widehat J}_z]$](img7299.gif) commutator pairs
shows that the angular momentum in the other two directions is zero
too. So there is no angular momentum at all,
commutator pairs
shows that the angular momentum in the other two directions is zero
too. So there is no angular momentum at all, 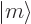 is
an
is
an 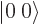 state.
state.
![]() ,
,![]()
![]() .
.![]()
![]()
![]()
![]()
![]() ,
,![]() -
-![]()
![]()
![]()
![]()