| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.25 Number of boson states
For identical bosons, the number is 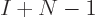 choose
choose 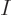 . To see
that think of the
. To see
that think of the 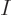 bosons as being inside a series of
bosons as being inside a series of 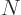 single
particle-state
single
particle-state boxes.
The idea is as illustrated in
figure D.2; the circles are the bosons and the thin lines
separate the boxes. In the picture as shown, each term in the group
of states has one boson in the first single-particle function, three
bosons in the second, three bosons in the third, etcetera.
Figure D.2:
Bosons in single-particle-state boxes.
 |
Each picture of this type corresponds to exactly one system state. To
figure out how many different pictures there are, imagine there are
numbers written from 1 to 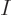 on the bosons and from
on the bosons and from 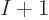 to
to 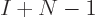 on the separators between the boxes. There are then
on the separators between the boxes. There are then 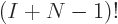 ways
to arrange that total of
ways
to arrange that total of 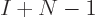 objects. (There are
objects. (There are 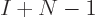 choices
for which object to put first, times
choices
for which object to put first, times 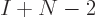 choices for which object
to put second, etcetera.) However, the
choices for which object
to put second, etcetera.) However, the 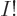 different ways to order
the subset of boson numbers do not produce different pictures if you
erase the numbers again, so divide by
different ways to order
the subset of boson numbers do not produce different pictures if you
erase the numbers again, so divide by 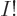 . The same way, the
different ways to order the subset of box separator numbers do not
make a difference, so divide by
. The same way, the
different ways to order the subset of box separator numbers do not
make a difference, so divide by 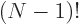 .
.
For example, if 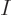
 2 and
2 and 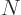
 4, you get 5!
4, you get 5! 2!3!
or 10 system states.
2!3!
or 10 system states.
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]() .
.![]()
![]()
![]()
![]()
![]()