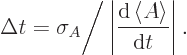A.18 The en­ergy-time un­cer­tainty re­la­tion­ship

As men­tioned in chap­ter 4.5.3, Heisen­berg’s for­mu­lae

$$\Delta{p_x}\Delta{x}\mathrel{\raisebox{-1pt}{$\geqslant$}}\frac12\hbar$$

re­lat­ing the typ­i­cal un­cer­tain­ties in mo­men­tum and po­si­tion is of­ten very con­ve­nient for qual­i­ta­tive de­scrip­tions of quan­tum me­chan­ics, es­pe­cially if you mis­read 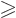$\raisebox{-.5pt}{$\geqslant$}$ as $\vphantom0\raisebox{1.1pt}{$\approx$}$.

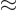So, tak­ing a cue from rel­a­tiv­ity, peo­ple would like to write a sim­i­lar ex­pres­sion for the un­cer­tainty in the time co­or­di­nate,

$$\Delta{E}\Delta{t}\mathrel{\raisebox{-1pt}{$\geqslant$}}\frac12\hbar$$

The en­ergy un­cer­tainty can rea­son­ably be de­fined as the stan­dard de­vi­a­tion 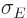$\sigma_E$ in en­ergy. How­ever, if you want to for­mally jus­tify the en­ergy-time re­la­tion­ship, it is not at all ob­vi­ous what to make of that un­cer­tainty in time 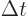$\Delta{t}$.

To ar­rive at one de­f­i­n­i­tion, as­sume that the vari­able of real in­ter­est in a given prob­lem has a time-in­vari­ant op­er­a­tor $A$. The gen­er­al­ized un­cer­tainty re­la­tion­ship of chap­ter 4.5.2 be­tween the un­cer­tain­ties in en­ergy and $A$ is then:

$$\sigma_E \sigma_A \mathrel{\raisebox{-1pt}{$\geqslant$}}\frac12\vert\langle[H,A]\rangle\vert.$$

But ac­cord­ing to chap­ter 7.2 $\vert\langle[H,A]\rangle\vert$ is just $\hbar\vert{\rm d}\langle{A}\rangle/{\rm d}{t}\vert$.

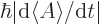So the Man­delsh­tam-Tamm ver­sion of the en­ergy-time un­cer­tainty re­la­tion­ship just de­fines the un­cer­tainty in time to be

$$\Delta t = \sigma_A\Bigg/\left\vert\frac{{\rm d}\left\langle{A}\right\rangle }{{\rm d}t}\right\vert.$$

That cor­re­sponds to the typ­i­cal time in which the ex­pec­ta­tion value of $A$ changes by one stan­dard de­vi­a­tion. In other words, it is the time that it takes for $A$ to change to a value suf­fi­ciently dif­fer­ent that it will clearly show up in mea­sure­ments.