| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.18 Eigenfunctions of commuting operators
Any two operators  and
and 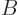 that commute,
that commute, 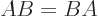 , have a common set
of eigenfunctions, provided only that each has a complete set of
eigenfunctions. (In other words, the operators do not necessarily
have to be Hermitian. Unitary, anti-Hermitian, etcetera, operators
all qualify.)
, have a common set
of eigenfunctions, provided only that each has a complete set of
eigenfunctions. (In other words, the operators do not necessarily
have to be Hermitian. Unitary, anti-Hermitian, etcetera, operators
all qualify.)
First note the following:
if 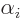 is an eigenfunction of
is an eigenfunction of  with eigenvalue
with eigenvalue 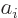 , then
, then
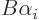 is either also an eigenfunction of
is either also an eigenfunction of  with eigenvalue
with eigenvalue
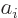 or is zero.
or is zero.
To see that, note that since  and
and 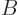 commute
commute 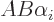

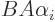 which is
which is 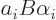 . Comparing start and end, the
combination
. Comparing start and end, the
combination 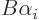 must be an eigenfunction of
must be an eigenfunction of  with
eigenvalue
with
eigenvalue 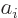 if it is not zero. (Eigenfunctions may not be zero.)
if it is not zero. (Eigenfunctions may not be zero.)
Now assume that there is just a single independent eigenfunction
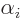 for each distinct eigenvalue
for each distinct eigenvalue 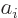 of
of  . Then if
. Then if
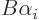 is nonzero, it can only be a multiple of that single
eigenfunction. By definition, that makes
is nonzero, it can only be a multiple of that single
eigenfunction. By definition, that makes 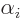 an eigenfunction
of
an eigenfunction
of 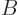 too, with as eigenvalue the multiple. On the other hand, if
too, with as eigenvalue the multiple. On the other hand, if
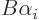 is zero, then
is zero, then 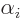 is still an eigenfunction of
is still an eigenfunction of 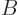 ,
now with eigenvalue zero. So under the stated assumption,
,
now with eigenvalue zero. So under the stated assumption,  and
and 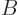 have the exact same eigenfunctions, proving the assertion of this
derivation.
have the exact same eigenfunctions, proving the assertion of this
derivation.
However, frequently there is degeneracy,
i.e. there is
more than one eigenfunction 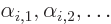 for a
single eigenvalue
for a
single eigenvalue 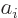 . Then the fact that, say,
. Then the fact that, say, 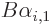 is
an eigenfunction of
is
an eigenfunction of  with eigenvalue
with eigenvalue 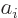 no longer means that
no longer means that
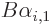 is a multiple of
is a multiple of 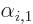 ; it only means that
; it only means that
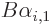 is some combination of all of
is some combination of all of
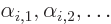 . Which means that
. Which means that 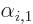 is not in general an eigenfunction of
is not in general an eigenfunction of 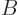 .
.
To deal with that, it has to be assumed that the problem has been
numerically approximated by some finite-dimensional one. Then  and
and 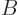 will be matrices, and the number of independent eigenfunctions (or
rather, eigenvectors now) of
will be matrices, and the number of independent eigenfunctions (or
rather, eigenvectors now) of  and
and 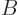 will be finite and equal.
That allows the problem to be addressed one eigenfunction at a time.
will be finite and equal.
That allows the problem to be addressed one eigenfunction at a time.
Assume now that 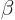 is an eigenfunction of
is an eigenfunction of 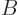 , with eigenvalue
, with eigenvalue
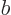 , that is not yet an eigenfunction of
, that is not yet an eigenfunction of  too. By completeness, it
can still be written as a combination of the eigenfunctions of
too. By completeness, it
can still be written as a combination of the eigenfunctions of  ,
and more particularly as
,
and more particularly as 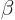

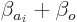 where
where
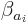 is a combination of the eigenfunctions of
is a combination of the eigenfunctions of  with
eigenvalue
with
eigenvalue 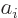 and
and 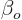 a combination of the eigenfunctions of
a combination of the eigenfunctions of
 with other eigenvalues. There must be such eigenfunctions with
with other eigenvalues. There must be such eigenfunctions with
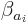 nonzero, because without using the
nonzero, because without using the 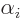 you cannot
create an equal number of independent eigenfunctions of
you cannot
create an equal number of independent eigenfunctions of 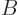 as of
as of  .
By definition
.
By definition
but that must mean that
since if it is not, 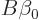 cannot make up the difference; as seen
earlier,
cannot make up the difference; as seen
earlier, 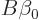 only consists of eigenfunctions of
only consists of eigenfunctions of  that do
not have eigenvalue
that do
not have eigenvalue 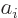 . According to the above equation,
. According to the above equation,
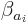 , which is already an eigenfunction of
, which is already an eigenfunction of  with
eigenvalue
with
eigenvalue 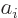 , is also an eigenfunction of
, is also an eigenfunction of 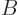 with eigenvalue
with eigenvalue 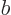 .
So replace one of the
.
So replace one of the 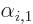 ,
, 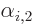 ,...with
,...with
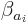 . (If you write
. (If you write 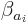 in terms of the
in terms of the
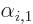 ,
, 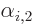 ,..., then the function you replace
may not appear with a zero coefficient.) Similarly replace an
eigenfunction of
,..., then the function you replace
may not appear with a zero coefficient.) Similarly replace an
eigenfunction of 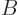 with eigenvalue
with eigenvalue 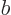 with
with 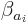 . Then
. Then  and
and 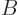 have one more common eigenfunction. Keep going in this way
and eventually all eigenfunctions of
have one more common eigenfunction. Keep going in this way
and eventually all eigenfunctions of 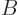 are also eigenfunctions of
are also eigenfunctions of
 and vice versa.
and vice versa.
Similar arguments can be used recursively to show that more generally,
a set of operators 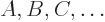 that all commute have a single
common set of eigenfunctions. The trick is to define an artificial
new operator, call it
that all commute have a single
common set of eigenfunctions. The trick is to define an artificial
new operator, call it 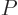 , that has the common eigenfunctions of
, that has the common eigenfunctions of  and
and 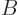 , but whose eigenvalues are distinct for any two eigenfunctions
unless these eigenfunctions have the same eigenvalues for both
, but whose eigenvalues are distinct for any two eigenfunctions
unless these eigenfunctions have the same eigenvalues for both  and
and
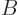 . Then the eigenfunctions of
. Then the eigenfunctions of 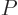 , even if you mess with them,
remain eigenfunctions of
, even if you mess with them,
remain eigenfunctions of  and
and 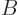 . So go find common
eigenfunctions for
. So go find common
eigenfunctions for 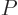 and
and 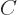 .
.
The above derivation assumed that the problem was finite-dimensional, or
discretized some way into a finite-dimensional one like you do in numerical
solutions. The latter is open to some suspicion, because even the
most accurate numerical approximation is never truly exact.
Unfortunately, in the infinite-dimensional case the derivation gets much
trickier. However, as the hydrogen atom and harmonic oscillator
eigenfunction examples indicate, typical infinite systems in nature do
obey the theorem anyway.
![]()
![]()
![]() ,
,,
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() ;
;![]()
![]() .
.![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() ,
,![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]() ,
,![]()
![]() ,
,![]()
![]() .
.![]() ,
,![]()
![]() .
.![]()
![]() .
.