| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.48 About Lagrangian multipliers
This note will derive the Lagrangian multipliers for an example
problem. Only calculus will be used. The example problem will be to
find a stationary point of a function 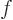 of four variables if there
are two constraints. Different numbers of variables and constraints
would work out in similar ways as this example.
of four variables if there
are two constraints. Different numbers of variables and constraints
would work out in similar ways as this example.
The four variables that example function 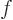 depends on will be
denoted by
depends on will be
denoted by 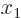 ,
, 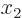 ,
, 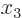 , and
, and 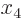 .
The two constraints will be taken to be equations of the form
.
The two constraints will be taken to be equations of the form
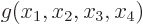
 0 and
0 and 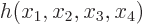
 0, for
suitable functions
0, for
suitable functions 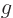 and
and 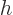 . Constraints can always be
brought in such a form by taking everything in the constraint’s
equation to the left-hand side of the equals sign.
. Constraints can always be
brought in such a form by taking everything in the constraint’s
equation to the left-hand side of the equals sign.
So the example problem is:
Stationarize means to find locations where the function has a minimum
or a maximum, or any other point where it does not change under small
changes of the variables 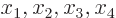 as long as these satisfy
the constraints.
as long as these satisfy
the constraints.
The first thing to note is that rather than considering 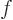 to be a
function of
to be a
function of 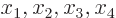 , you can consider it instead to be
to be a function of
, you can consider it instead to be
to be a function of 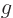 and
and 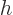 and only two additional variables from
and only two additional variables from
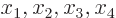 , say
, say 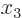 and
and 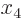 :
:
The reason you can do that is that you should in principle be able to
reconstruct the two missing variables 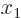 and
and 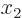 given
given 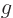 ,
,
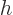 ,
, 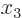 , and
, and 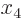 .
.
As a result, any small change in the function 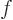 , regardless of
constraints, can be written using the expression for a total
differential as:
, regardless of
constraints, can be written using the expression for a total
differential as:
At the desired stationary point, acceptable changes in variables are
those that keep 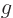 and
and 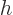 constant at zero; they have
constant at zero; they have 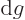
 0 and
0 and
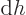
 0. So for
0. So for 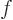 to be stationary under all acceptable changes
of variables, you must have that the final two terms are zero for any
changes in variables. This means that the partial derivatives in the
final two terms must be zero since the changes
to be stationary under all acceptable changes
of variables, you must have that the final two terms are zero for any
changes in variables. This means that the partial derivatives in the
final two terms must be zero since the changes 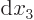 and
and
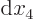 can be arbitrary.
can be arbitrary.
For changes in variables that do go out of bounds, the change in 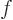 will not be zero; that change will be given by the first two
terms in the right-hand side. So, the erroneous changes in
will not be zero; that change will be given by the first two
terms in the right-hand side. So, the erroneous changes in 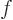 due to
going out of bounds are these first two terms, and if we subtract
them, we get zero net change for any arbitrary change in
variables:
due to
going out of bounds are these first two terms, and if we subtract
them, we get zero net change for any arbitrary change in
variables:
In other words, if we penalize
the change in 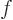 for
going out of bounds by amounts
for
going out of bounds by amounts 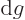 and
and 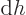 at the rate above,
any change in variables will produce a penalized change of zero,
whether it stays within bounds or not.
at the rate above,
any change in variables will produce a penalized change of zero,
whether it stays within bounds or not.
The two derivatives at the stationary point in the expression above
are the Lagrangian multipliers or penalty factors, call them
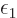

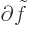

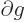 and
and 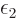

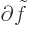

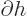 . In those terms
. In those terms
for whatever is the change in the variables 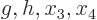 , and
that means for whatever is the change in the original variables
, and
that means for whatever is the change in the original variables
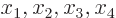 . Therefore, the change in the penalized
function
. Therefore, the change in the penalized
function
is zero whatever is the change in the variables
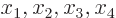 .
.
In practical application, explicitly computing the Lagrangian
multipliers 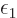 and
and 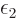 as the derivatives of
function
as the derivatives of
function 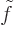 is not needed. You get four equations by putting
the derivatives of the penalized
is not needed. You get four equations by putting
the derivatives of the penalized 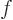 with respect to
with respect to 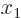 through
through
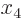 equal to zero, and the two constraints provide two more
equations. Six equations is enough to find the six unknowns
equal to zero, and the two constraints provide two more
equations. Six equations is enough to find the six unknowns 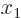 through
through 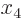 ,
, 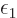 and
and 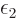 .
.
![]()
![]()
![]() ,
,![]() ,
,![]() ,
,![]() .
.![]()
![]()
![]()
![]()
![]()
![]() .
.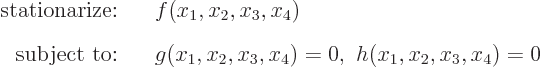
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]() :
:![]() ,
,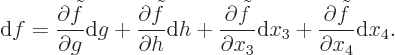
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
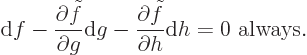
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]() .
.