| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.79 Derivation of perturbation theory
This note derives the perturbation theory results for the solution of
the eigenvalue problem 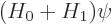

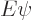 where
where 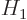 is small.
The considerations for degenerate problems use linear algebra.
is small.
The considerations for degenerate problems use linear algebra.
First, small
is not a valid mathematical term. There
are no small numbers in mathematics, just numbers that become zero in
some limit. Therefore, to mathematically analyze the problem, the
perturbation Hamiltonian will be written as
where  is some chosen number that physically indicates
the magnitude of the perturbation potential. For example, if the
perturbation is an external electric field,
is some chosen number that physically indicates
the magnitude of the perturbation potential. For example, if the
perturbation is an external electric field,  could be
taken as the reference magnitude of the electric field. In
perturbation analysis,
could be
taken as the reference magnitude of the electric field. In
perturbation analysis,  is assumed to be vanishingly
small.
is assumed to be vanishingly
small.
The idea is now to start with a good eigenfunction 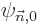 of
of
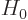 , (where
, (where good
is still to be defined), and
correct it so that it becomes an eigenfunction of 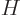

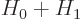 . To do so, both the desired energy eigenfunction and
its energy eigenvalue are expanded in a power series in terms of
. To do so, both the desired energy eigenfunction and
its energy eigenvalue are expanded in a power series in terms of
 :
:
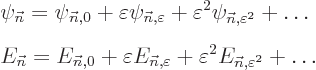
If  is a small quantity, then
is a small quantity, then 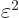 will be
much smaller still, and can probably be ignored. If not, then surely
will be
much smaller still, and can probably be ignored. If not, then surely
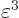 will be so small that it can be ignored. A result
that forgets about powers of
will be so small that it can be ignored. A result
that forgets about powers of  higher than one is called
first order perturbation theory. A result that also includes the
quadratic powers, but forgets about powers higher than two is called
second order perturbation theory, etcetera.
higher than one is called
first order perturbation theory. A result that also includes the
quadratic powers, but forgets about powers higher than two is called
second order perturbation theory, etcetera.
Before proceeding with the practical application, a disclaimer is
needed. While it is relatively easy to see that the eigenvalues
expand in whole powers of  , (note that they must be
real whether
, (note that they must be
real whether  is positive or negative), it is much more
messy to show that the eigenfunctions must expand in whole powers. In
fact, for degenerate energies
is positive or negative), it is much more
messy to show that the eigenfunctions must expand in whole powers. In
fact, for degenerate energies 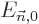 they only do if you choose
good states
they only do if you choose
good states 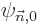 . See Rellich’s lecture notes on
Perturbation Theory [Gordon & Breach, 1969] for a proof. As a result
the problem with degeneracy becomes that the good unperturbed
eigenfunction
. See Rellich’s lecture notes on
Perturbation Theory [Gordon & Breach, 1969] for a proof. As a result
the problem with degeneracy becomes that the good unperturbed
eigenfunction 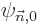 is initially unknown. It leads to lots
of messiness in the procedures for degenerate eigenvalues described
below.
is initially unknown. It leads to lots
of messiness in the procedures for degenerate eigenvalues described
below.
When the above power series are substituted into the eigenvalue
problem to be solved,
the net coefficient of every power of  must be
equal in the left and right hand sides. Collecting these coefficients
and rearranging them appropriately produces:
must be
equal in the left and right hand sides. Collecting these coefficients
and rearranging them appropriately produces:
These are the equations to be solved in succession to give the various
terms in the expansion for the wave function 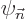 and the energy
and the energy
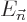 . The further you go down the list, the better your
combined result should be.
. The further you go down the list, the better your
combined result should be.
Note that all it takes is to solve problems of the form
The equations for the unknown functions are in terms of the
unperturbed Hamiltonian 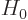 , with some additional but in
principle knowable terms.
, with some additional but in
principle knowable terms.
For difficult perturbation problems like you find in engineering, the
use of a small parameter  is essential to get the
mathematics right. But in the simple applications in quantum
mechanics, it is usually overkill. So most of the time the expansions
are written without, like
is essential to get the
mathematics right. But in the simple applications in quantum
mechanics, it is usually overkill. So most of the time the expansions
are written without, like
where you are assumed to just imagine that 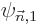 and
and
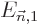 are
are first order small,
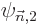 and
and 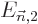 are “second order
small,” etcetera. In those terms, the successive equations to
solve are:
are “second order
small,” etcetera. In those terms, the successive equations to
solve are:
| | |
|
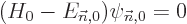 | |
(D.55) |
| | |
|
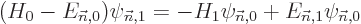 | |
(D.56) |
| | |
|
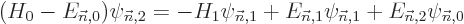 | |
(D.57) |
| | |
|
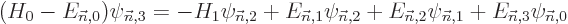 | |
(D.58) |
| | |
|
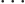 | |
|
Now consider each of these equations in turn. First, (D.55)
is just the Hamiltonian eigenvalue problem for 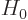 and is already
satisfied by the chosen unperturbed solution
and is already
satisfied by the chosen unperturbed solution 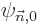 and its
eigenvalue
and its
eigenvalue 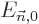 . However, the remaining equations are
not trivial. To solve them, write their solutions in terms of the
other eigenfunctions
. However, the remaining equations are
not trivial. To solve them, write their solutions in terms of the
other eigenfunctions 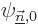 of the unperturbed
Hamiltonian
of the unperturbed
Hamiltonian 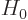 . In particular, to solve (D.56),
write
. In particular, to solve (D.56),
write
where the coefficients 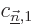 are still to be determined. The
coefficient of
are still to be determined. The
coefficient of 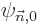 is zero on account of the normalization
requirement. (And in fact, it is easiest to take the coefficient of
is zero on account of the normalization
requirement. (And in fact, it is easiest to take the coefficient of
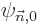 also zero for
also zero for 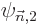 ,
,
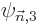 , ..., even if it means that the resulting wave
function will no longer be normalized.)
, ..., even if it means that the resulting wave
function will no longer be normalized.)
The problem (D.56) becomes
where the left hand side was cleaned up using the fact that the
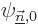 are eigenfunctions of
are eigenfunctions of 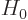 . To get the first
order energy correction
. To get the first
order energy correction 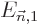 , the trick is now to take an
inner product of the entire equation with
, the trick is now to take an
inner product of the entire equation with
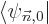 . Because of the fact that the energy
eigenfunctions of
. Because of the fact that the energy
eigenfunctions of 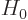 are orthonormal, this inner product produces
zero in the left hand side, and in the right hand side it produces:
are orthonormal, this inner product produces
zero in the left hand side, and in the right hand side it produces:
And that is exactly the first order correction to the energy claimed
in {A.38.1}; 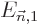 equals the Hamiltonian
perturbation coefficient
equals the Hamiltonian
perturbation coefficient 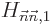 . If the problem is not
degenerate or
. If the problem is not
degenerate or 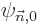 is good, that is.
is good, that is.
To get the coefficients 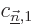 , so that you know what is
the first order correction
, so that you know what is
the first order correction 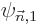 to the wave function, just
take an inner product with each of the other eigenfunctions
to the wave function, just
take an inner product with each of the other eigenfunctions
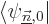 of
of 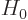 in turn. In the left hand side it
only leaves the coefficient of the selected eigenfunction because of
orthonormality, and for the same reason, in the right hand side the
final term drops out. The result is
in turn. In the left hand side it
only leaves the coefficient of the selected eigenfunction because of
orthonormality, and for the same reason, in the right hand side the
final term drops out. The result is
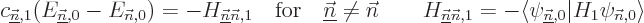
The coefficients 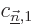 can normally be computed
from this.
can normally be computed
from this.
Note however that if the problem is degenerate, there will be
eigenfunctions 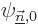 that have the same energy
that have the same energy 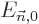 as the eigenfunction
as the eigenfunction 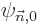 being corrected. For these the
left hand side in the equation above is zero, and the equation cannot
in general be satisfied. If so, it means that the assumption that an
eigenfunction
being corrected. For these the
left hand side in the equation above is zero, and the equation cannot
in general be satisfied. If so, it means that the assumption that an
eigenfunction 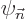 of the full Hamiltonian expands in a power
series in
of the full Hamiltonian expands in a power
series in  starting from
starting from 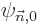 is untrue.
Eigenfunction
is untrue.
Eigenfunction 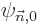 is bad. And that means that the first
order energy correction derived above is simply wrong. To fix the
problem, what needs to be done is to identify the submatrix of all
Hamiltonian perturbation coefficients in which both unperturbed
eigenfunctions have the energy
is bad. And that means that the first
order energy correction derived above is simply wrong. To fix the
problem, what needs to be done is to identify the submatrix of all
Hamiltonian perturbation coefficients in which both unperturbed
eigenfunctions have the energy 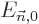 , i.e. the submatrix
, i.e. the submatrix
The eigenvalues of this submatrix are the correct first order energy
changes. So, if all you want is the first order energy changes, you
can stop here. Otherwise, you need to replace the unperturbed
eigenfunctions that have energy 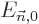 . For each
orthonormal eigenvector
. For each
orthonormal eigenvector 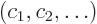 of the submatrix, there is
a corresponding replacement unperturbed eigenfunction
of the submatrix, there is
a corresponding replacement unperturbed eigenfunction
You will need to rewrite the Hamiltonian perturbation coefficients in
terms of these new eigenfunctions. (Since the replacement
eigenfunctions are linear combinations of the old ones, no new
integrations are needed.) You then need to reselect the eigenfunction
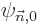 whose energy to correct from among these replacement
eigenfunctions. Choose the first order energy change (eigenvalue of
the submatrix)
whose energy to correct from among these replacement
eigenfunctions. Choose the first order energy change (eigenvalue of
the submatrix) 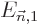 that is of interest to you and then choose
that is of interest to you and then choose
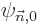 as the replacement eigenfunction corresponding to a
corresponding eigenvector. If the first order energy change
as the replacement eigenfunction corresponding to a
corresponding eigenvector. If the first order energy change
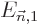 is not degenerate, the eigenvector is unique, so
is not degenerate, the eigenvector is unique, so
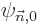 is now good. If not, the good eigenfunction will be
some combination of the replacement eigenfunctions that have that
first order energy change, and the good combination will have to be
figured out later in the analysis. In any case, the problem with the
equation above for the
is now good. If not, the good eigenfunction will be
some combination of the replacement eigenfunctions that have that
first order energy change, and the good combination will have to be
figured out later in the analysis. In any case, the problem with the
equation above for the 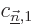 will be fixed, because the new
submatrix will be a diagonal one:
will be fixed, because the new
submatrix will be a diagonal one: 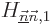 will be zero when
will be zero when
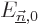

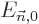 and
and 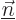
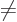
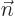 . The
coefficients
. The
coefficients 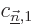 for which
for which 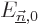

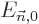 remain indeterminate at this stage. They will normally be found at a
later stage in the expansion.
remain indeterminate at this stage. They will normally be found at a
later stage in the expansion.
With the coefficients 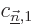 as found, or not
found, the sum for the first order perturbation
as found, or not
found, the sum for the first order perturbation 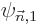 in
the wave function becomes
in
the wave function becomes
The entire process repeats for higher order. In particular, to second
order (D.57) gives, writing 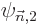 also in terms of the unperturbed eigenfunctions,
also in terms of the unperturbed eigenfunctions,
To get the second order contribution to the energy, take again an
inner product with 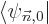 . That produces, again
using orthonormality, (and diagonality of the submatrix discussed
above if degenerate),
. That produces, again
using orthonormality, (and diagonality of the submatrix discussed
above if degenerate),
This gives the second order change in the energy stated in
{A.38.1}, if 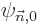 is good. Note that since
is good. Note that since
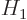 is Hermitian, the product of the two Hamiltonian perturbation
coefficients in the expression is just the square magnitude of either.
is Hermitian, the product of the two Hamiltonian perturbation
coefficients in the expression is just the square magnitude of either.
In the degenerate case, when taking an inner product with a
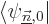 for which
for which 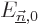

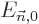 , the equation can be satisfied through the still
indeterminate
, the equation can be satisfied through the still
indeterminate 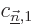 provided that the corresponding diagonal
coefficient
provided that the corresponding diagonal
coefficient 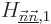 of the diagonalized submatrix is unequal
to
of the diagonalized submatrix is unequal
to 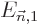

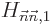 . In other words, provided
that the first order energy change is not degenerate. If that is
untrue, the higher order submatrix
. In other words, provided
that the first order energy change is not degenerate. If that is
untrue, the higher order submatrix
will need to be diagonalized, (the rest of the equation needs to be
zero). Its eigenvalues give the correct second order energy changes.
To proceed to still higher energy, reselect the eigenfunctions
following the same general lines as before. Obviously, in the
degenerate case the entire process can become very messy. And you may
never become sure about the good eigenfunction.
This problem can often be eliminated or greatly reduced if the
eigenfunctions of 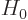 are also eigenfunctions of another operator
are also eigenfunctions of another operator
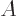 , and
, and 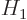 commutes with
commutes with 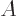 . Then you can arrange
the eigenfunctions
. Then you can arrange
the eigenfunctions 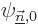 into sets that have the same value
for the
into sets that have the same value
for the good
quantum number 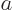 of
of 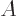 . You can
analyze the perturbed eigenfunctions in each of these sets while
completely ignoring the existence of eigenfunctions with different
values for quantum number
. You can
analyze the perturbed eigenfunctions in each of these sets while
completely ignoring the existence of eigenfunctions with different
values for quantum number 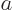 .
.
To see why, consider two example eigenfunctions 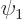 and
and 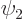 of
of 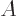 that have different eigenvalues
that have different eigenvalues 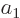 and
and 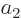 . Since
. Since
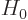 and
and 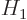 both commute with
both commute with 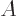 , their sum
, their sum 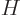 does, so
does, so
and since 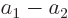 is not zero,
is not zero, 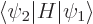 must
be. Now
must
be. Now 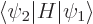 is the amount of
eigenfunction
is the amount of
eigenfunction 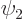 produced by applying
produced by applying 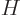 on
on 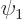 . It
follows that applying
. It
follows that applying 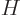 on an eigenfunction with an eigenvalue
on an eigenfunction with an eigenvalue 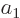 does not produce any eigenfunctions with different eigenvalues
does not produce any eigenfunctions with different eigenvalues
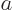 . Thus an eigenfunction of
. Thus an eigenfunction of 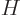 satisfying
satisfying
can be replaced by just 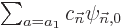 , since
this by itself must satisfy the eigenvalue problem: the Hamiltonian of
the second sum does not produce any amount of eigenfunctions in the
first sum and vice-versa. (There must always be at least one value of
, since
this by itself must satisfy the eigenvalue problem: the Hamiltonian of
the second sum does not produce any amount of eigenfunctions in the
first sum and vice-versa. (There must always be at least one value of
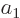 for which the first sum at
for which the first sum at 
 0 is independent
of the other eigenfunctions of
0 is independent
of the other eigenfunctions of 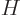 .) Reduce every eigenfunction
of
.) Reduce every eigenfunction
of 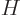 to an eigenfunction of
to an eigenfunction of 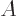 in this way. Now the existence of
eigenfunctions with different values of
in this way. Now the existence of
eigenfunctions with different values of 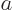 than the one being
analyzed can be ignored since the Hamiltonian does not produce them.
In terms of linear algebra, the Hamiltonian has been reduced to block
diagonal form, with each block corresponding to a set of
eigenfunctions with a single value of
than the one being
analyzed can be ignored since the Hamiltonian does not produce them.
In terms of linear algebra, the Hamiltonian has been reduced to block
diagonal form, with each block corresponding to a set of
eigenfunctions with a single value of 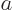 . If the Hamiltonian
also commutes with another operator
. If the Hamiltonian
also commutes with another operator 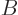 that the
that the 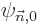 are
eigenfunctions of, the argument repeats for the subsets with a single
value for
are
eigenfunctions of, the argument repeats for the subsets with a single
value for 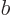 .
.
The Hamiltonian perturbation coefficient
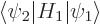 is zero whenever two good quantum
numbers
is zero whenever two good quantum
numbers 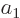 and
and 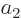 are unequal. The reason is the same as for
are unequal. The reason is the same as for
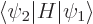 above. Only perturbation coefficients
for which all good quantum numbers are the same can be nonzero.
above. Only perturbation coefficients
for which all good quantum numbers are the same can be nonzero.
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() .
.![]() :
: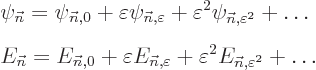
![]() ,
,![]()
![]()
![]() .
.![]()
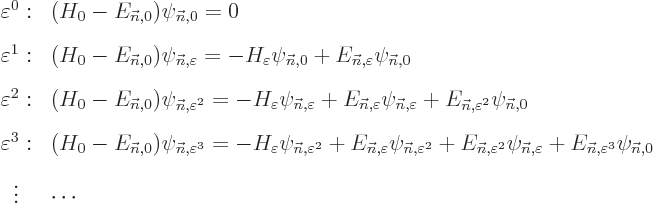
![]()
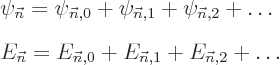
![]()
![]()
![]() .
.![]()
![]() .
.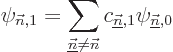
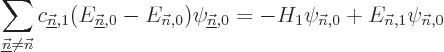
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
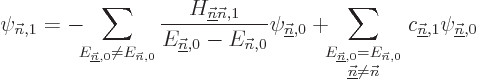
![]()
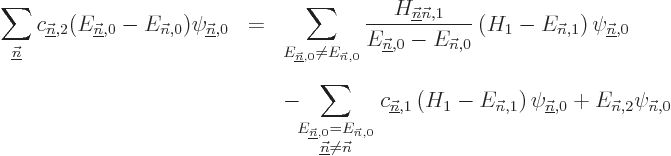
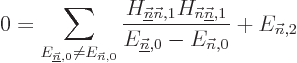
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() .
.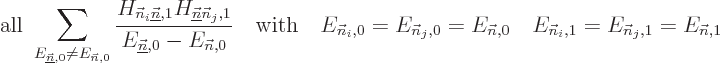
![]()
![]() ,
,![]()
![]() .
.![]()
![]()
![]() .
.![]() .
.![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]() ,
,![]()
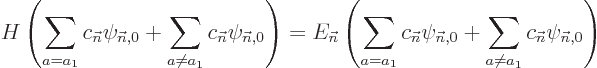
![]()
![]()
![]()
![]()