Stoke's Principle

After many years (from Newton's and Euler's time, to mid 19th century) of confusion and research, we arrievd at a set of postulates ( Stoke's Principle)

1. is s continous, linear function of , P, , T, , t, but not of

   

2. The fluid is homogeneous (i.e. explicitly)
3. The fluid is isotropic
4. If at rest the stress is hydrostatic pressure
5. If deformation is purely dilatation the average normal stress is equal to the hydrostatic pressure (Stoke's Hypothesis)

lets discuss the postualltion further: From 1: we may express the stress as

This is similar to an expansion of a function in polynomial

Here , , and From 2:(homogeneity) From 5: (if at rest is hydrostatic)

for a fluid at rest , then

for Newotonian fluids

Here are coefficients for viscous fluid model, in this case it has 81 terms. For example

Since reduced to 36 terms

From 4: (Isotropic) For isotropic tensor of 4th order we may write

then

Here , and are three scalar coefficients. Since , , then

therfore, the stress tensor becomes

Here is the rate of strain tensor. In components the stresses are

It should be remarked that the model coefficients are reduced from 81 to 2. They are the two viscosities the first viscosity and the second viscosity.

From 5:(Stoke's hypothesis)

pure dilatation. The average of normal stresses is

Stoke assumed that . Therefore

or

The derivation of Navier-Stokes' equations is now completed. In Cartesina tensor notation we have

where

is known as the stress deviator or

Now we can write the equations of motion as Continuity equation:

Momentum Equation:

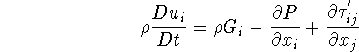
It should be marked that is an unknown coefficient known as viscosity. It is determined from experiment.