consider a volume 
let 
be the rate of energy got in
is the rate of energy increased in
is the rate of work done by on the surroundings. are from conduction +
radiation + heat source and sink. is the rate of increase of internal energy and kinetic energy.
is the work done by potential forces and work done by stress. From the first law of thermodynamics (
conservation of energy)
Work done by on the surrounding, can be written as
Note :
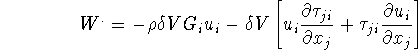
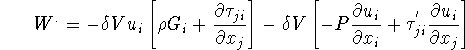
Energy increased in
e is the energy per unit mass.
Now
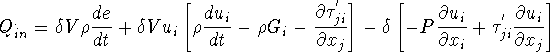
The first bracket is zero by Navier-Stokes equations thus,
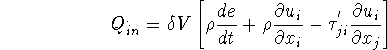
Rate of energy transferred into
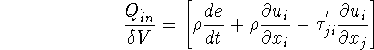
Net rate of heat conducted into in the x direction 
Similarly for the y and z directions. Thus,
Then
