There are essentially two parts to the theoretical background regarding the analysis of the distillation column in our laboratory. The first area of interest is predicting values of the bottoms and distillate ethanol mole fractions based on the number of theoretical stages measured at total reflux and the known feed, bottoms, reflux, and distillate flow rates for the various experimental runs. This boils down to predicting a separation based on a known number of stages as measured at total refluxs, n, and reflux ratio, R. These predictions afford the possibility of comparing the measured separation to a predicted separation to verify the validity of our model.
The second area of interest is determining a theoretical minimum number of stages and minimum reflux ratio based on the measured values of the bottoms and distillate ethanol mole fractions. This provides an opportunity to compare the theoretical minimum number of stages for a given separation to the number of stages determined at total reflux. The number of stages at total reflux, i.e. infinite reflux ratio, should always be less than the number of stages determined for a given separation and a finite reflux ratio. It is also useful to compare the calculated minimum reflux ratio to the actual reflux ratio calculated based on the reflux and distillate flow rates. The value of the minimum reflux ratio should always be less than the actual value.
An additional aspect of the theoretical background pertaining to this experiment is to present means of verifying the validity of our models. Overall and component mass balances may be applied to the experimental data to verify that the data satisfies the mass balances to a reasonable degree. In addition, it is useful to predict a value for the vaporization rate in the column based on the electric power to the reboiler and the heat of vaporization of our more volatile component, ethanol. This predicted value of the vaporization rate in the column may be compared to the measured vaporization rate determined based on the liquid reflux and distillate flow rates used in the laboratory. It is important to note that discrepancies that appear in these checks are likely attributed to incorrect flow rate values obtained from the rotameters. This is a topic that will be examined in great detail in the discussion section of the report.
The modeling of our system will be carried out using two methods: the McCabe-Thiele graphical methodology and the ChemCad computer simulation package. First we shall address the McCabe-Thiele method and all of the governing equations. In order to utilize the McCabe-Thiele method to predict a separation based on a known reflux ratio, it is necessary to determine the theoretical number of stages at total reflux. It is first necessary to develop the vapor equilibrium relations for the system. A fundamental relation for vapor and liquid phases in equilibrium is Raoult's Law (Geankoplis, p. 640):
![]() (1)
(1)
In regards to nomenclature, subscript A represents the more volatile component of the binary mixture, ethanol in this case, and subscript B represents the less volatile component, propanol in this case. Vapor-liquid equilibrium data is the key element to performing the analysis being described. Vapor-liquid equilibrium diagrams utilized in the analysis are typically an xy plot that features the liquid and vapor mole fractions of the component of interest. A useful relation is the relative volatility of component A with respect to component B. This relation is given below (Geankoplis p. 645):
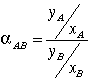 (2)
(2)
It is often useful to calculate the average relative volatility of the distillate and bottoms section of the apparatus. A relation that may be used to calculate the average relative volatility of the light key component used in determining the minimum number of stages required for a given separation is the following:
![]() (3)
(3)
Equation (3) gives the last piece of information necessary to calculate the theoretical minimum number of stages using the Fenske equation:
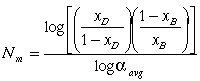 (4)
(4)
.Equation (4) provides one way of calculating the number of stages at total reflux. At total reflux, all the vapor going up the column is condensed and sent down again while all the liquid running into the reboiler is evaporated. The number of stages may also be determined graphically using the McCabe-Thiele stepwise methodology. The first step of the McCabe-Thiele method for determining the minimum number of stages is to draw the equilibrium line on the ethanol x-y plot.
The second step of the is to draw the y = x line.
The third step of the McCabe-Thiele method for total reflux is to plot the measured bottoms and distillate ethanol mole fractions along the y = x line. For total reflux, the y = x line represents the operating line for the column. The final step is to perform a stepping off procedure in which a horizontal line is drawn from the distillate mole fraction on the operating line to the equilibrium line, followed by a vertical line drawn back down to the operating line. This stepping off is repeated until the desired bottoms composition is reached. Steps three and four are summarized in the figure below.
While on the topic of total reflux conditions in the column, it is useful to calculate the overall efficiency and the Murphree vapor efficiency. The overall efficiency is determined by inserting the number of theoretical plates calculated at total reflux, it is important to note that this value is the number of stages calculated using equation (4) minus one plate for the reboiler, into the following relation:
![]() (5)
(5)
Equation ( ) is used to calculate the Murphree vapor efficiency, EMV.
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
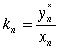 (9)
(9)
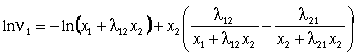 (10)
(10)
Using the number of stages at total reflux, it is possible to solve the "operating" problem for the distillation column. This procedure is slightly different than the typical "design" problem of determining the necessary size of the column (number of trays) and required reflux ratio to achieve a desired separation. The known quantities used in this procedure are the number of stages measured at total reflux, reflux ratio, feed rate, feed composition, quality of the feed, and electric power to the reboiler. As in all predictive calculations, the idea is to take the values of the independent variables set for the experiment and generate predictions of the dependent variables to be measured. The reflux ratio is defined as:
![]() (11)
(11)
The overall mole balance is given in equation (12) below.
![]() (12)
(12)
In equation (1), F is the feed molar flow rate, D is the distillate molar flow rate and B is the bottoms flow rate. The species mole balance can also be developed.
![]() (13)
(13)
In equation (13), the more volatile component is taken as a basis (in this case ethanol), so xF is the mole fraction of ethanol in the feed, xD is the mole fraction of ethanol in the distillate, and xB is the mole fraction of ethanol in the bottoms. The first step to predicting the distillate and bottoms mole fractions is to estimate the molar vaporization rate in the column. A reasonable estimate for the molar vaporization rate is provided by the following relation:
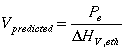 (14)
(14)
Pe is the electric power to the reboiler and is defined by the following relation:
![]() (15)
(15)
At this point it is useful to include a summary of the significant physical properties of the components in our system over the relevant temperature range. The following table presents the enthalpy of vaporization of ethanol, as well as the density of the ethanol and propanol mixture at the various temperatures of interest.
Table 1: The enthalpy of vaporization of ethanol and density of a 40/60 by mass ethanol and propanol mixture.
|
Temperature (oC) |
DHvap,Eth*10-7 (J/kmol) |
Density - rmix (kmol/m3) |
|
70 |
3.93 |
13.95 |
|
75 |
3.89 |
13.85 |
|
80 |
3.85 |
13.76 |
|
85 |
3.81 |
13.67 |
|
90 |
3.77 |
13.57 |
For the purposes of checking the consistency of the experimental data and to qualitatively determine whether or not heat losses are a factor for our system, it is useful to calculate the measured vaporization rate. This is merely the sum of the measured molar liquid reflux rate and distillate rate.
![]() (16)
(16)
Returning to the predictive methodology, the next step is to estimate the distillate molar flow rate. This is accomplished by inserting the estimated vaporization rate calculated from equation (14) and the known reflux ration into the following relation:
![]() (17)
(17)
The liquid molar reflux rate can be estimated by inserting the predicted vaporization rate and the known reflux ration into the following relation:
![]() (18)
(18)
The bottoms flow rate is estimated based on the known feed flow rate and the predicted bottoms flow rate. This is accomplished by inserting the known feed flow rate and the predicted distillate flow rate calculated using equation (17) into equation (12), the overall mole balance.
We have now
estimated all of the necessary quantities to allow for the prediction
of the bottoms and distillate ethanol mole fractions. We must first
guess a value of xD and insert it into equation
(13), the overall species mole balance, along with the known feed
mole fraction and the predicted bottoms and distillate flow rates.
This generates a prediction for the bottoms ethanol mole fraction
along with the guess of the distillate mole fraction. From this
point it is matter of drawing up the McCabe-Thiele plot and verifying
that the predicted distillate and bottoms composition correspond to
the number of stages calculated at total reflux. The first two
graphical steps are similar to the total reflux procedure, drawing
the operating and y = x lines. The first graphical step to be
presented for this procedure is to plot the guessed xD
value along the y = x line and connect it to the point
![]() along the y axis. The xD used in the previous
relation is the value guessed in the prediction, not the
experimentally determined value. This line is the operating line for
the rectifying section of the column. This is illustrated in Figures
4 and 5 below.
along the y axis. The xD used in the previous
relation is the value guessed in the prediction, not the
experimentally determined value. This line is the operating line for
the rectifying section of the column. This is illustrated in Figures
4 and 5 below.
The next step in the graphical procedure is to construct the operating line for the stripping section of the column. This is accomplished by plotting the predicted value of xB along the y = x line and drawing a line through the point where the rectifying line intersects the feed line. This step is summarized below in Figure 5.
The final step in solving the "operating" problem with the McCabe-Thiele method is to stage off the number of stages determined at total reflux and verifies that it matches the predicted values of the distillate and bottoms ethanol mole fractions. If the predicted values of the bottoms and distillate mole fractions do not correspond to the number of stages, the procedure must be repeated until the condition is satisfied. An example plot showing convergence on predicted compositions is shown below in Figure 6.
For cases involving feed and a finite reflux ratio, it is useful to calculate the theoretical minimum number of stages for the measured separation. This is accomplished using equation (4). It is also of use to calculate the minimum reflux ratio for the separation. This is accomplished using the following relation:
![]() (19)
(19)
An alternative method of determining the theoretical minimum number of stages for a measured separation is to solve the "design" problem using the McCabe-Thiele model. This procedure utilizes the measured bottoms and distillate mole fractions, as well as the known reflux ratio to graphically determine the theoretical minimum number of stages. In explaining this method it is useful to develop the balances for individual parts of the column. The rectifying section is considered first. Assuming the column is operating at steady state, the following mole balances are written between the nth stage and the top of the column.
![]() (20)
(20)
![]() (21)
(21)
In equations (20) and (21) above, V is the vapor flux and L is the liquid flux and both are assumed constant between the top of the column and the nth plate. In equation (21), xn and yn are defined as the liquid and vapor mole fractions of the more volatile component respectively on the nth stage, while y1 and xo are the composition of the vapor leaving the first stage and the composition of the liquid entering the first stage respectively. Rearranging equation (21) reveals the linear relationship between the vapor composition on the (n+1)th plate to the liquid composition on the nth plate.
![]() (22)
(22)
A similar equation may be written for the stripping section of the column where the flow rates are G' and L' for the vapor and liquid respectively and N is the total number of trays.
![]() (23)
(23)
In equation (23), yN+1 is the vapor composition entering the bottom of the column and xN is the liquid composition leaving that stage.
Assuming that the column has a total condenser, the vapor composition y1 leaving the top plate will equal the liquid composition entering the top plate xo. Then the following relationships develop.
![]() (24)
(24)
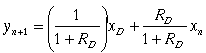 (25)
(25)
Equation (25) is a combination of equations (16) and (22) where RD
is the reflux ratio
![]() .
Equation (25) is the operating line for the rectifying section.
.
Equation (25) is the operating line for the rectifying section.
Next, the operating line for the stripping section must be determined. Assuming the vapor and liquid are in equilibrium, the reboiler can be considered an extra stage. Performing the same type of simplification as above, the following relations develop.
![]() (26)
(26)
![]() (27)
(27)
![]() (28)
(28)
Equation (28) is the operating line for the stripping section.
The next step in calculating the number of theoretical stages is to determine the feed line or "q-line". At the intersection of the two operating lines, xn and yn+1 have the same values in both the stripping and rectifying sections. Thus, the difference between the equations for the stripping and rectifying section of the column is necessary.
![]() (29)
(29)
Rewriting in terms of the feed:
![]() (30)
(30)
![]() (31)
(31)
Equation (31) defines q as the moles of liquid produced per mole of feed. Rearranging gives (L-L')=(-qF). From the overall balance of the feed stage we see that:
![]() (32)
(32)
![]() (33)
(33)
By combining equations (33) and (30), a new feed line can be developed which gives the intersection of the two operating lines.
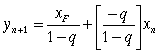 (34)
(34)
Equation (34) represents a straight line passing through the point (xF, xF). Now, we have all the tools needed to determine the theoretical number of stages.
The
McCabe-Thiele method of calculating the number of theoretical stages
is a geometric method, which utilizes both the operating lines, the
equilibrium line, and the feed line. The procedure begins by
plotting the equilibrium line. Next, the feed line is drawn through
the point (xF, xF). Thirdly, the
intercept of the operating line for the rectifying portion of the
column is calculated from equation (25). This is equal to
![]() as previously mentioned in the description of the "operating"
problem. The operating line is then drawn connecting the intercept
with the point (xD, yD).
Finally, the operating line for the stripper section is drawn from
the intercept of the first operating line with the feed line to the
point (xB, yB) in the same
fashion as described for the "operating" problem. Now, the
number of stages is determined using the stepwise procedure
illustrated below in figures 1 - 4. The process ends when the
desired bottoms composition, xB, is reached.
as previously mentioned in the description of the "operating"
problem. The operating line is then drawn connecting the intercept
with the point (xD, yD).
Finally, the operating line for the stripper section is drawn from
the intercept of the first operating line with the feed line to the
point (xB, yB) in the same
fashion as described for the "operating" problem. Now, the
number of stages is determined using the stepwise procedure
illustrated below in figures 1 - 4. The process ends when the
desired bottoms composition, xB, is reached.
(