- 1.
- Note that a ``one-degree-of-freedom'' system is one in which the motion
is described by one coordinate (e.g., x). Examples
- 2.
- Sketch Figure 10.1(a).
- 3.
- Derive the equation
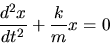
below, using Newton's second law. (Remember to first draw the free body
diagram.)
- 4.
- Notice that in this chapter the acceleration is represented by
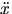 as opposed to simply a. This is because we desire the differential
equation describing the motion at any time t as opposed
to simply determining the acceleration at a particular instant in
time.
as opposed to simply a. This is because we desire the differential
equation describing the motion at any time t as opposed
to simply determining the acceleration at a particular instant in
time.
- 5.
- Sketch Figure 10.1(c).
- 6.
- Derive the equation
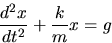
below, using Newton's second law.
- 7.
- Make the change of variable
 and show that
and show that 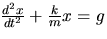 is equivalent to
is equivalent to
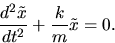
vspace2.0in
Solutions
- 8.
- Consider the homogeneous, linear, ordinary differential equation
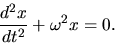
. Why is this equation considered ordinary?
Why is this equation considered linear?
Why is this equations considered homogeneous?
- 9.
- For the above spring-mass systems, what is
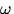 ?
?
- 10.
- By substitution, show that
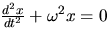 is satisfied by
is satisfied by
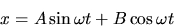
where A and B are arbitrary constants.
- 11.
- Show that
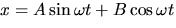 is equivalent to
is equivalent to
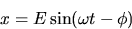
where E and 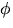 are constants, by using a standard trigonometric identity to rewrite
are constants, by using a standard trigonometric identity to rewrite 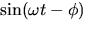 .
.
- 12.
- Write A and B in terms of E and
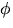 .
.
- 13.
- Note that
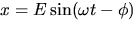 is useful for plotting x as a function of time t. This expression
clearly demonstrates the oscillatory nature of the motion. This motion
is called
is useful for plotting x as a function of time t. This expression
clearly demonstrates the oscillatory nature of the motion. This motion
is called 

 .
.
- 14.
- Sketch x vs. t and clearly label E and
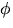 on the plot.
on the plot.
- 15.
- The constant
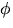 is called the
is called the  of the response, while E is called the
of the response, while E is called the  of the response.
of the response.
- 16.
- Note that
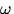 is the natural frequency of the system in units of radians per sec.
The natural frequency in units of cycles per sec is denoted by f
where
is the natural frequency of the system in units of radians per sec.
The natural frequency in units of cycles per sec is denoted by f
where

The period of vibration in units of seconds is denoted by 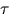 where
where
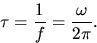
(The book does not call 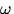 a natural frequency so this discussion differs slightly from that in the
book.)
a natural frequency so this discussion differs slightly from that in the
book.)
This section may be covered in a class lecture.
This section may be covered in a class lecture.
![]()
![]()
![]()
![]()
![]()
![]()
![]() are constants, by using a standard trigonometric identity to rewrite
are constants, by using a standard trigonometric identity to rewrite ![]() .
.
![]()
![]() where
where ![]()
![]() a natural frequency so this discussion differs slightly from that in the
book.)
a natural frequency so this discussion differs slightly from that in the
book.)