Chapter 2
- 1.
- To design a vehicle, an engineer must be able to
 and
and  its motion.
its motion.
- 2.
- In this chapter we are not concerned with the
 of motion. We merely want to
of motion. We merely want to  and
and  the motion of a point in space.
the motion of a point in space.
- 3.
- For a moving object this point might be the


 .
. - 4.
- Another name for path is
 .
. - 5.
- Important. Always (in your notes and completion of the reading journal) denote vectors by an overbar, e.g.,
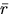 . In the book vectors are denoted by only bold, e.g.,
. In the book vectors are denoted by only bold, e.g., 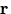 , whereas in this reading journal vectors are denoted by both bold and an overbar, e.g.,
, whereas in this reading journal vectors are denoted by both bold and an overbar, e.g., 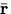 .
.
- 1.
- Sketch Figure 2.1(a) and (b) below.
- 2.
- It is assumed that
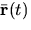 is the position vector from O to P. Write a simple expression for
is the position vector from O to P. Write a simple expression for 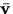 , the velocity of P relative to O at time t. (Your answer should be in terms of a derivative.)
, the velocity of P relative to O at time t. (Your answer should be in terms of a derivative.)
- 3.
- Write the definition of a derivative
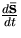 of a vector
of a vector 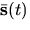 .
.
- 4.
- Suppose
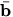 and
and 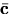 are vector functions of time (i.e.,
are vector functions of time (i.e., 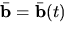 and
and 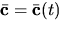 ). Fill in the right hand side of the following:
). Fill in the right hand side of the following:

- 5.
- Suppose
 is a scalar function of time (i.e.,
is a scalar function of time (i.e., 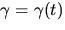 ) and
) and 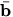 is a vector function of time (i.e.,
is a vector function of time (i.e., 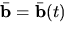 ). Fill in the right hand side of the following:
). Fill in the right hand side of the following:

- 6.
- Write a simple expression for
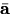 , the acceleration of P relative to O at time t. (Your answer should be in terms of a derivative.)
, the acceleration of P relative to O at time t. (Your answer should be in terms of a derivative.)
- 7.
- Important. In this class scalars and vectors are often functions of time but this dependence is not explicitly recognized. You must learn to recognize (from the context) when a quantity is a function of time.
- 8.
- Important. In this class scalars and vectors are often functions of time but this dependence is not explicitly recognized. You must learn to recognize (from the context) when a quantity is a function of time. (This repeat is not a typo.)
- 1.
- List at least four examples of straight line motion.
- 1.
- Sketch Figure 2.3(a) and (b) below (side-by-side). Important: Here and everywhere below, denote the unit vector by
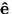 although the book does not use the ``hat''. (Of course, you can only use the hat and not the bold.)
although the book does not use the ``hat''. (Of course, you can only use the hat and not the bold.)
- 2.
- Fill in the right hand side of the following equations, following the book exactly. (However, unlike the book, denote the unit vector by
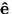 .)
.)
Make sure that you understand each of the above steps!
- 3.
- For straight line motion, the reason we can represent the position, velocity and acceleration by the scalars s, v and a is that the position vector, the velocity vector, and the acceleration vector are each in the direction described by the unit vector
 .
. - 4.
- Sketch Figures 2.4 and 2.5 below (side-by-side).
- 5.
- Make sure that you understand the graphical interpretation of the derivative expressions for v(t) and a(t) as given by the above figures. That is, given a curve of s(t) can you compute (or at least estimate) v at a given time, and given a curve of v(t) can you compute or estimate a at a given time?
- 1.
- Sketch Figure 2.6 below.
- 2.
- Suppose t has units of seconds and
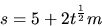
Fill in the right hand side of the following equations. (Make sure you write the units.)
Acceleration Specified as a Function of Time
- 3.
- Suppose that we know the acceleration a(t). Use indefinite integration to derive an expression for the velocity v. Label the equation for v ``(1)'' and denote the unknown constant by A.
- 4.
- Now, suppose that we know the velocity v(t). Use indefinite integration to derive an expression for the position s. Label the equation for s ``(2)'' and denote the unknown constant by B.
- 5.
- Describe the additional information we would need to determine the constants A and B in (1) and (2).
- 6.
- Now, assume v(t0)=v0 and use definite integration to derive an expression for the velocity v. Label the equation for v ``(3)''.
- 7.
- Assume s(t0)=s0 and use definite integration to derive an expression for the position s. Label the equation for s ``(4)''.
- 8.
- Sketch Figures 2.7(a) and (b) below (side-by-side).
- 9.
- Make sure that you understand the graphical interpretation of the integral expressions for v(t) and s(t) as given by the above figures. That is, given a graph of a(t), cay you compute or estimate v(t)-v(t0) from this graph? Likewise, given a graph of v(t), can you compute or estimate s(t)-s(t0) from this graph?
- 10.
- If one neglects aerodynamic
 , then it can be assumed that an apple dropped from a tree at about sea level has constant acceleration.
, then it can be assumed that an apple dropped from a tree at about sea level has constant acceleration.
- 11.
- Assume that the acceleration a is a known constant a0. Then, solve the integrals in (3) and (4) to obtain expressions for v and s as functions of time. Label these equations respectively ``(5)'' and ``(6)''.
- 12.
- Use the chain rule to express the acceleration a (not necessarily constant) purely in terms of a derivative with respect to s.
- 13.
- Fill in the missing step leading to the following integral expression.
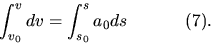
- 14.
- Now assume that a is equal to the constant a0. Integrate both sides of the above equation.
- 15.
- Danger Will Robinson; Danger!! Equations (5) thru (7) are valid only when the acceleration is
 .
.
- 1.
- For straight line motion, the position vector
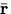 , velocity vector
, velocity vector 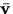 , and acceleration vector
, and acceleration vector 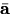 are described completely by the scalars s, v, and a respectively, since the directions of these vectors are parallel to a straight line. However, for curvilinear motion the direction of motion varies so we must be careful to describe both the
are described completely by the scalars s, v, and a respectively, since the directions of these vectors are parallel to a straight line. However, for curvilinear motion the direction of motion varies so we must be careful to describe both the  and
and  of these vectors.
of these vectors.
- 1.
- Sketch Figure 2.15 below.
- 2.
- Following the book, fill in the right hand side of the following equations.


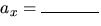 ,
,
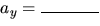 ,
,
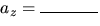 .
.
Make sure that you understand each of the above steps.
- 3.
- For a projectile problem in which the projectile moves in the x-y plane,
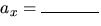 ,
, 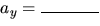 , and
, and 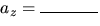 .
. - 4.
- Sketch Figure 2.16 below.
- 5.
- Suppose the above figure describes the initial condition of a projectile. Derive an expressions for x and box in your final answer.
- 6.
- Now, derive an expressions for y and box in your final answer.
- 7.
- Using your above expressions for x and y, derive an expression for y as a function of x.
- 1.
- Sketch Figure 2.18 below.
- 2.
- The angular velocity
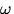 of L relative to L0 is defined by,
of L relative to L0 is defined by,

- 3.
- The angular acceleration
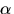 of L relative to L0 is defined by,
of L relative to L0 is defined by,

- 4.
- Write the contents of Table 2.2 below to enforce the fact that the equations of straight-line motion and angular motion are identical in form.
Straight-Line Motion Angular Motion
- 1.
- Sketch Figure 2.19(a) below and at the tip of
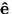 sketch the unit vector
sketch the unit vector 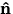 .
.
- 2.
- The unit vector
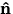 is
is  to
to 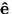 and points in the
and points in the  .
.
- 1.
- Sketch Figure 2.22 below.
- 2.
- The unit vector
 is
is  to the path in the direction of motion.
to the path in the direction of motion.
- 3.
- The unit vectors
 and
and 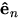 correspond respectively to
correspond respectively to 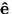 and
and 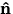 above (under the heading ``Rotating Unit Vector''). Hence,
above (under the heading ``Rotating Unit Vector''). Hence, 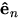 is
is  to
to  and is in the positive
and is in the positive 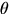 direction.
direction.
- 4.
- Write the expression for the velocity vector of P in terms of v and
 .
.
- 5.
- Sketch Figure 2.24 below.
- 6.
- Referring to the above figure, the instantaneous radius of curvature is the distance
 .
. - 7.
- Write the expression for the acceleration vector of P in terms of
v,
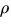 ,
,  , and
, and 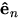 .
.
- 8.
- Summarize the results by rewriting equations (2.38) thru (2.40) below.
Sketch Figure 2.27 below.
Following the book complete the following equations.
- 1.
- Sketch Figure 2.31(a) and (b) below (side-by-side).
- 2.
- Write the expression for the position vector
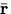 in terms of r and
in terms of r and 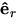 .
.
- 3.
- Now, differentiate this expression for
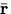 and use the fact that
and use the fact that 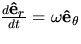 to derive an expression for the velocity vector
to derive an expression for the velocity vector 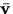 in terms of r,
in terms of r, 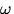 ,
, 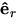 , and
, and 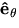 .
.
- 4.
- Next, differentiate the expression for
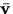 , and use the additional facts that
, and use the additional facts that 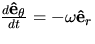 and
and 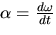 to derive an expression for the acceleration vector
to derive an expression for the acceleration vector 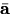 in terms of r, v,
in terms of r, v, 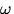 ,
, 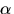 ,
, 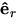 , and
, and 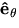 . Express your final answer in the form
. Express your final answer in the form 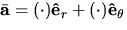 .
.
- 5.
- Summarize this subsection by writing equations (2.49) thru (2.51) below.
Sketch Figures 2.35(a) and (b) below (side-by-side).
Write 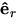 in terms of
in terms of 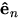 and
and 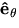 in terms of
in terms of  .
.
For circular motion, r is equal to the constant R. Hence the velocity expression in polar coordinates becomes,

In normal and tangential components, the velocity vector is 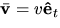 . Hence, comparing these two expressions for
. Hence, comparing these two expressions for 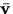 (and using equations
(and using equations  and
and  ), an expression for v in terms of R and
), an expression for v in terms of R and 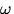 is
is
v = .
For circular motion, the acceleration expression in polar coordinates becomes,

In normal and tangential components, the acceleration vector is 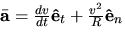 . Hence, equating the transverse and tangential components of the two expressions for
. Hence, equating the transverse and tangential components of the two expressions for 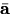 (and and using equations
(and and using equations  and
and  ),
),
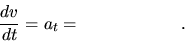
Polar coordinates describe the motion of a point P in  dimensional motion (i.e., in the x-y plane). Cylindrical coordinates are used to describe
dimensional motion (i.e., in the x-y plane). Cylindrical coordinates are used to describe  dimensional motion.
dimensional motion.
Sketch Figure 2.36 below.
Summarize the formulas for cylindrical coordinates below by writing equations (2.52) thru (2.55) from the text.
The expression for 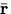 in cylindrical coordinates differs from that for polar coordinates by the addition of the term
in cylindrical coordinates differs from that for polar coordinates by the addition of the term  . The expression for
. The expression for 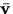 in cylindrical coordinates differs from that for polar coordinates by the addition of the term
in cylindrical coordinates differs from that for polar coordinates by the addition of the term  . The expression for
. The expression for 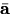 in cylindrical coordinates differs from that for polar coordinates by the addition of the term
in cylindrical coordinates differs from that for polar coordinates by the addition of the term  .
.
This section may or may not be covered as will be mentioned in class.
- 1.
- Sketch Figure 2.46 below.
- 2.
- Write
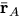 in terms of
in terms of 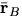 and
and 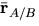 .
.
- 3.
- Differentiate the above expression to write
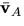 in terms of
in terms of 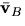 and
and 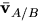 .
.
- 4.
- Differentiate the above expression to write
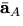 in terms of
in terms of 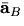 and
and 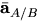 .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]() ,
, ![]() .
.
![]()
![]()
![]() in terms of
in terms of ![]() and
and ![]() in terms of
in terms of ![]() .
.![]()
![]() . Hence, comparing these two expressions for
. Hence, comparing these two expressions for ![]() (and using equations
(and using equations ![]() and
and ![]() ), an expression for v in terms of R and
), an expression for v in terms of R and ![]() is
is
![]()
![]() . Hence, equating the transverse and tangential components of the two expressions for
. Hence, equating the transverse and tangential components of the two expressions for ![]() (and and using equations
(and and using equations ![]() and
and ![]() ),
),
![]()
![]() dimensional motion (i.e., in the x-y plane). Cylindrical coordinates are used to describe
dimensional motion (i.e., in the x-y plane). Cylindrical coordinates are used to describe ![]() dimensional motion.
dimensional motion.
![]() in cylindrical coordinates differs from that for polar coordinates by the addition of the term
in cylindrical coordinates differs from that for polar coordinates by the addition of the term ![]() . The expression for
. The expression for ![]() in cylindrical coordinates differs from that for polar coordinates by the addition of the term
in cylindrical coordinates differs from that for polar coordinates by the addition of the term ![]() . The expression for
. The expression for ![]() in cylindrical coordinates differs from that for polar coordinates by the addition of the term
in cylindrical coordinates differs from that for polar coordinates by the addition of the term ![]() .
.