Chapter 3

Force, Mass, and Acceleration

Force, Mass, and Acceleration

1.
Describe the fundamental difference between this chapter and Chapter 2.







Newton's Second Law

1.
Using the appropriate mathematical symbols (e.g., m), the linear momentum of a particle = $\rule{0.5in}{.01in}$.
2.
Write Newton's second law for a particle in terms of the rate of change of the particle's linear momentum.



3.
Simplify the above expression if the particle's mass is constant.



4.
Using Newton's second law, you can determine a particle's motion, specifically $\rule{1.4in}{.01in}$, when you know the $\rule{1.0in}{.01in}$ acting on it.


Inertial Reference Frames

1.
When dealing with ``down to earth problems,'' the acceleration term in Newton's second law can be expressed in terms of a reference frame that is fixed relative to the $\rule{1.0in}{.01in}$.
2.
When dealing with ``down to earth problems,'' the acceleration term in Newton's second law     can     cannot      be expressed in terms of a reference frame that is rotating or one that is accelerating relative to the earth.

3.
Give the text's definition of an inertial reference frame.







Equation of Motion for the Center of Mass

1.
Consider a collection of N particles which have masses m1, m2, ..., mN. Write an expression for the total mass m in terms of the individual masses.



2.
If the position of the 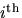$i^{\rm th}$ particle is denoted by 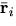$\mbox{$\bar{{\bf r}}$}_i$, what is the mathematical expression for the center of mass 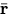$\mbox{$\bar{{\bf r}}$}$ of this collection of particles.





3.
You are expected to commit to memory the expression for the center of mass. This should be easy if you simply recognize that the center of mass is the average position of the masses of the collection of particles.

4.
For a collection of particles the text shows that

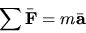
\begin{displaymath} \sum\mbox{$\bar{\bf F}$}= m\mbox{$\bar{{\bf a}}$}\end{displaymath}

where 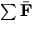$\sum\mbox{$\bar{\bf F}$}$ is the sum of the external forces. This expression is also referred to as ``Newton's second law'' although it is actually a derivative of Newton's second law. In the derivation of this expression the internal forces (i.e., the forces between particles) are introduced. Explain why only the external forces appear in the final equation.






Applications

Cartesian Coordinates and Straight-Line Motion

1.
Write Newton's second law using cartesian coordinates.





2.
Write the three corresponding scalar equations of motion.





3.
If the particle is confined to straight-line motion along the x axis, write the simplification of the scalar equations.



4.
Consider Example 3.2 and assume that block A slips. On a separate piece of paper draw the free body diagram of block A and write the two scalar equations of motion.

Normal and Tangential Components

5.
Write Newton's second law using normal and tangential components.





where





6.
Write the two corresponding scalar equations of motion.





Polar Coordinates

7.
Write Newton's second law using polar coordinates.





where









8.
Write the two corresponding scalar equations of motion.









Chapter Summary

Read this section.