Chapter 5

Momentum Methods

1.
The principle of impulse and momentum allows one to determine the change in an object's $\rule{1.0in}{.01in}$ when the external forces are known as functions of $\rule{1.0in}{.01in}$.

Principle of Impulse and Momentum

1.
Write the equation describing the principle of impulse and momentum.





2.
The integral on the left is the linear impulse while 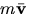$m\mbox{$\bar{{\bf v}}$}$ is the $\rule{1.0in}{.01in}$ $\rule{1.0in}{.01in}$.

3.
Write the equation describing 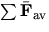$\sum\mbox{$\bar{\bf F}$}_{\rm av}$, the average with respect to time of the total force acting on an object from t1 to t2, in terms of the linear momentum.




4.
Describe an impulsive force.







Conservation of Linear Momentum

1.
If the effects of external forces can be neglected, $\rule{1.0in}{.01in}$ $\rule{1.0in}{.01in}$ is conserved. This conservation principle allows one to analyze interactions between particles, such as $\rule{1.0in}{.01in}$.
2.
Sketch Figure 5.5.












3.
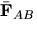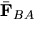Write the relationship between $\mbox{$\bar{\bf F}$}_{AB}$ and $\mbox{$\bar{\bf F}$}_{BA}$.




4.
Write the principle of impulse and momentum for each object for arbitrary times t1 and t2.









5.
Write the conservation of linear momentum equation obtained by summing the above two equations.



6.
This result may also be written as

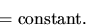
\begin{displaymath} ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ = {\rm constant}.\end{displaymath}

7.
Sketch Figure 5.6.












8.
Write the equation describing the position vector 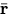$\mbox{$\bar{{\bf r}}$}$ of the combined center of mass in terms of the position vectors of objects A and B.





9.
Taking the time derivative of this equation and using the conservation of momentum yields

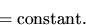
\begin{displaymath} ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ = {\rm constant}.\end{displaymath}

10.
Do the conservation of momentum equations apply in some cases in which significant external forces act on objects A and B? Explain your answer.









11.
Conservation equations     apply     do not apply      to an arbitrary number of objects. (Circle the correct answer.)

Impacts

1.
Objects A and B undergo a perfectly plastic impact if they $\rule{1.0in}{.01in}$ $\rule{1.0in}{.01in}$ after they collide.
2.
Describe a very nice feature of collisions that are perfectly plastic.






3.
For collisions that are not perfectly plastic, linear momentum conservation     is     is not     sufficient to determine their velocities after the impact. (Circle the correct answer)


Direct Central Impacts

4.
Describe direct central impact.









5.
Write the equation describing the coefficient of restitution.









6.
What happens during the time interval from t1 to tC?






7.
What happens during the time interval from tC to t2?






8.
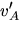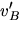Write an equation for the coefficient of restitution in terms of the vA and vB, the velocities before impact, and $v_A^\prime$ and $v_B^\prime$, the velocities after impact.







Oblique Central Impacts

9.
What is an oblique impact?












Angular Momentum

1.
Sketch Figure 5.14(a).












2.
Write the equation describing the principle of angular impulse and momentum.





3.
The integral on the left is the angular impulse while 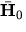$\mbox{$\bar{\bf H}$}_0$ is the $\rule{1.0in}{.01in}$ $\rule{1.0in}{.01in}$.


Central-Force Motion

4.
Describe what it means for an object to be in central force motion.









5.
What is the center of motion?






6.
$\rule{1.0in}{.01in}$ $\rule{1.0in}{.01in}$ are the most familiar instances of central-force motion.

7.
In central force motion

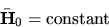
\begin{displaymath} \mbox{$\bar{\bf H}$}_0 = {\rm constant}\end{displaymath}

such that angular momentum is conserved. Explain why this holds.






Mass Flows

This section may not be covered in this class.


Chapter Summary

Read this section.