Chapter 7

Two-Dimensional Dynamics of Rigid Bodies

1.
What new equations are derived in this chapter?

Preview of the Equations of Motion

1.
Write Newton's second law.



2.
Sketch Figure 7.1.













3.
Write the equation of angular motion for a rigid body rotating about a fixed axis O.



where I0 is the $\rule{1.0in}{.01in}$ $\rule{1.0in}{.01in}$ $\rule{0.4in}{.01in}$ $\rule{1.0in}{.01in}$ of the rigid body about O.

4.
Write the equation of angular motion for a rigid body in general planar motion.



where I is the $\rule{1.0in}{.01in}$ $\rule{1.0in}{.01in}$ $\rule{0.4in}{.01in}$ $\rule{1.0in}{.01in}$ of the rigid body about O.


Momentum Principles for a System of Particles

Force-Linear Momentum Principle

1.
For a collection of particles the text shows that

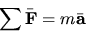
\begin{displaymath} \sum\mbox{$\bar{\bf F}$}= m\mbox{$\bar{{\bf a}}$}\end{displaymath}

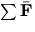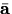where $\sum\mbox{$\bar{\bf F}$}$ is the sum of the $\rule{1.0in}{.01in}$ forces and $\mbox{$\bar{{\bf a}}$}$ is the acceleration of the $\rule{1.0in}{.01in}$ $\rule{0.4in}{.01in}$ $\rule{1.0in}{.01in}$. In the derivation of this expression the internal forces (i.e., the forces between particles) are introduced. Explain why only the external forces appear in the final equation.






Moment-Angular Momentum Principles

2.
Write the vector form of the equation of angular motion for a rigid body in general planar motion in terms of the moments 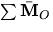$\sum\mbox{$\bar{\bf M}$}_O$ about a point O and the angular momentum 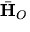$\mbox{$\bar{\bf H}$}_O$ about O.





3.
Write the vector form equation of the equation of angular motion for a rigid body in general planar motion in terms of the moments 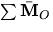$\sum\mbox{$\bar{\bf M}$}_O$ about a point O and the angular momentum 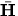$\mbox{$\bar{\bf H}$}$ about the center of mass.





4.
Write the vector form equation of the equation of angular motion for a rigid body in general planar motion in terms of the moments 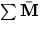$\sum\mbox{$\bar{\bf M}$}$ about the center of mass and the angular momentum 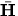$\mbox{$\bar{\bf H}$}$ about the center of mass.





Derivation of the Equations of Motion

1.
Write Newton's second law.



Rotation About a Fixed Axis

2.
Write the equation of angular motion (7.14).





Describe how this scalar equation was derived from the vector equation (7.11).





3.
Assume that an object can be viewed as a collection of N particles with masses mi and position vectors 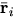$\mbox{$\bar{{\bf r}}$}_i$ measured from O. Write the definition of the moment of inertia IO about O.





4.
Express HO in terms of IO.



5.
Write the equation of angular motion for a rigid body in pure rotation in terms of the moments 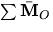$\sum\mbox{$\bar{\bf M}$}_O$ about the rotational point O and the moment of inertial IO about O.



General Planar Motion

6.
Write the scalar equation of angular motion corresponding to equation (7.13).





7.
Assume that an object can be viewed as a collection of N particles of masses mi and and position vectors 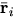$\mbox{$\bar{{\bf r}}$}_i$ measured from the center of mass. Write the definition of the moment of inertia I about the center of mass.





8.
Express H in terms of I.



9.
Write the equation of angular motion for a rigid body in general planar motion in terms of the moments 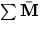$\sum\mbox{$\bar{\bf M}$}$ about the center of mass and the moment of inertia I about the center of mass.



Applications

1.
Write Newton's second law.



2.
Write the equation of angular motion for a rigid body rotating about a fixed axis O.



3.
Write the equation of angular motion for a rigid body in general planar motion.



4.
Write the three typical steps used to solve dynamics problems involving the above equations.












D'Alembert's Principle

1.
D'Alembert's principle is essentially a restatement of Newton's second laws. Write the ``D'Alembert'' equation below.



Appendix: Moments of Inertia

1.
Sketch Figures 7.29(b).












2.
Previously, the moment of inertia about a point O has been defined as

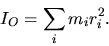
\begin{displaymath} I_O = \sum_i m_i r_i^2.\end{displaymath}

However, for objects consisting of a continuous distribution of mass (and not simply a collection of a finite number of mass particles) the moment of inertia is more precisely expressed in terms of an integral. Write this integral.





3.
Describe the meaning of r in the above equation.







Chapter Summary

Read this section.