Chapter 8

Energy and Momentum in Planar Rigid-Body Dynamics

1.
If the forces on an object are known as functions of position, you can use the principle of $\rule{1.0in}{.01in}$ $\rule{0.5in}{.01in}$ $\rule{1.0in}{.01in}$ to determine an object's       velocity vector       velocity magnitude as a function of position. (Circle the correct answer(s)).
2.
If the forces on an object are known as functions of time, you can use the principle of $\rule{1.0in}{.01in}$ $\rule{0.5in}{.01in}$ $\rule{1.0in}{.01in}$ to determine an object's       velocity vector       velocity magnitude as a function of time. (Circle the correct answer(s)).


Principle of Work and Energy

1.
Write the mathematical equation for the principle of work and energy for a rigid body.



2.
In the above equation U represents the $\rule{1.0in}{.01in}$ done by the $\rule{1.0in}{.01in}$ forces and $\rule{1.0in}{.01in}$ as the rigid body moves from $\rule{1.0in}{.01in}$ 1 to $\rule{1.0in}{.01in}$ 2. T denotes the $\rule{1.0in}{.01in}$ energy of the rigid body.


3.
Write the mathematical expression for T.



4.
In the above equation v is the $\rule{1.0in}{.01in}$ of the velocity of the $\rule{1.0in}{.01in}$ $\rule{0.4in}{.01in}$ $\rule{1.0in}{.01in}$ and I is the mass moment of inertia about the $\rule{1.0in}{.01in}$ $\rule{0.4in}{.01in}$ $\rule{1.0in}{.01in}$.

5.
Although, the above expression for T is valid for all types of rigid body motion, for rotation about a fixed axis O, write a simpler equation for T.



6.
Describe what IO denotes in the above eqution.





Systems of Particles

7.
For a system of particles the principle of work and energy is also given by U=T2-T1. However, U has a slightly different interpretation than it does for rigid bodies. That is U represents the work done on the system by both the $\rule{1.0in}{.01in}$ and external forces.

Rigid Body in Planar Motion

8.
The work done on a rigid body by $\rule{1.0in}{.01in}$ forces is zero.


9.
The above statement is proved in the text. To help understand the proof, first sketch Figure 8.2 below.












10.
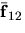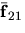The work done by the two forces $\mbox{$\bar{{\bf f}}$}_{12}$ and $\mbox{$\bar{{\bf f}}$}_{21}$ that the particles exert on each other is given by 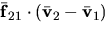$\mbox{$\bar{{\bf f}}$}_{21}\cdot(\mbox{$\bar{{\bf v}}$}_2-\mbox{$\bar{{\bf v}}$}_1)$. Describe using words and/or equations, how the book shows that this work is zero.









11.
State the principle of work and energy for a rigid body in words.






12.
State this principle for a system of rigid bodies.






13.
Describe the difference in the work in the above two statements of the principle of work and energy.






Kinetic Energy in General Plane Motion

14.
This subsection derives the expression

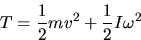
\begin{displaymath} T=\frac{1}{2}mv^2+\frac{1}{2}I\omega^2\end{displaymath}

. The first term represents the $\rule{1.4in}{.01in}$ $\rule{1.0in}{.01in}$ $\rule{1.0in}{.01in}$ while the second term represents the $\rule{1.4in}{.01in}$ $\rule{1.0in}{.01in}$ $\rule{1.0in}{.01in}$.

15.
To help understand the derivation of the above expression for T, first sketch Figure 8.3 below.












16.
Write equation (8.9) below.





What does 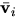$\mbox{$\bar{{\bf v}}$}_i$ denote in the above equation?






17.
Rewrite 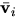$\mbox{$\bar{{\bf v}}$}_i$ in terms of 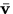$\mbox{$\bar{{\bf v}}$}$, the velocity of the $\rule{1.0in}{.01in}$ $\rule{0.4in}{.01in}$ $\rule{1.0in}{.01in}$.





18.
Describe 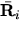$\mbox{$\bar{\bf R}$}_i$ in words.





19.
Write the expression for 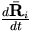$\frac{d\mbox{$\bar{\bf R}$}_i}{dt}$ used to derive the equation $T=\frac{1}{2}mv^2+\frac{1}{2}I\omega^2$.





20.
In the above expression 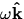$\omega\mbox{$\bf{\hat k}$}$ represents the $\rule{1.0in}{.01in}$ $\rule{1.0in}{.01in}$ $\rule{1.0in}{.01in}$ of the rigid body.

Kinetic Energy in Fixed Axis Rotation

21.
Sketch Figure 8.6(a).













22.
For rotation about a fixed axis this subsection derives the expression

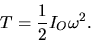
\begin{displaymath} T=\frac{1}{2}I_O\omega^2.\end{displaymath}

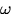This expression is derived from the more general expression $T=\frac{1}{2}mv^2+\frac{1}{2}I\omega^2$ by using the parallel axis theorem. The key step in expressing v, the magnitude of the velocity of the center of mass, in terms of $\omega$. Write this expression below.



23.
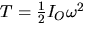Use the above expression to complete the derivation of $ T=\frac{1}{2}I_O\omega^2$.









Work and Potential Energy

1.
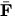Write the integral expression for the work U done on a rigid body by a force $\mbox{$\bar{\bf F}$}$.





2.
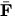If $\mbox{$\bar{\bf F}$}$ is a conservative force, it must satisfy a basic relation in terms of a potential energy V. Write this relation.



3.
Write the work U done by a conservative force in terms of its potential energy V.





4.
Sketch Figures 8.8(a) and (b) below (side-by-side).












5.
Express the couple magnitude M in terms of F, the magnitude of the forces.



6.
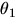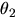Write the integral expression describing the work done by a couple M as the rigid body rotates from $\theta_1$ to $\theta_2$ in the direction of M.





7.
Write the simplification of the above expression for a constant couple M.



8.
If M is a conservative couple, it must satisfy a basic relation in terms of a potential energy V. Write this relation.



9.
Write the work U done by a conservative couple in terms of its potential energy V.





10.
Sketch Figure 8.9.












11.
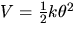For the linear torsional spring of the above figure derive the equation $V=\frac{1}{2}k\theta^2$.












12.
Suppose that all of the forces and couples that do work on a rigid body are conservative. Then the total work U may be expressed in terms of the total potential energy of the forces and couples. Write this mathematical expression for U below.



13.
Substituting the above expression into U=V1-V2 gives

T2+V2 =                       ,

which implies that

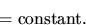
\begin{displaymath} ~~~~~~~~~~~~~~~~~~~~~~~ = {\rm constant}.\end{displaymath}

Power

1.
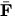Write an expression for the power P transmitted to a rigid body by a force $\mbox{$\bar{\bf F}$}$.



2.
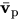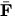In the above expression $\mbox{$\bar{{\bf v}}$}_{\rm p}$ is the velocity of the $\rule{1.0in}{.01in}$ $\rule{0.4in}{.01in}$ $\rule{1.0in}{.01in}$ of the force $\mbox{$\bar{\bf F}$}$.

3.
Write an expression for the power P transmitted to a rigid body by a couple M.



4.
Write an expression for the power P in terms of T, the kinetic energy of the rigid body.

5.
Write an expression for 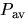$P_{\rm av}$, the average power transmitted to the rigid body during an interval of time from t1 to t2, in terms of T.





6.
Write an expression for 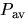$P_{\rm av}$ in terms of U.





7.
At the bottom of p. 375 a three step procedure for the application of energy methods is given. These three steps are repeated below with some accompanying questions for you to answer.
(a)
Identify the forces and couples that do work. What must first be drawn before identifying these forces and couples?



(b)
Apply work and energy or conservation of energy. Which of these two principles may always be used and describe when one may use the remaining principle.






(c)
Determine kinematic relationships. This often requires one to relate two quantities. What are these quantities?





Principles of Impulse and Momentum

1.
The principles of linear impulse and momentum and angular impulse and momentum relate $\rule{1.0in}{.01in}$ $\rule{1.0in}{.01in}$ of the forces and couples acting on a rigid body to changes in the $\rule{1.0in}{.01in}$ of the center of mass and the $\rule{1.0in}{.01in}$ $\rule{1.0in}{.01in}$ of the rigid body.
2.
These principles can be used to determine the effects of $\rule{1.0in}{.01in}$ forces and couples on the velocity of a rigid body. They may also be used to determine the velocities of the centers of mass and the angular velocities of objects after they undergo $\rule{1.0in}{.01in}$.

Linear Momentum

3.
Write the equation describing the principle of linear impulse and momentum for a rigid body.





4.
Describe how this equation is derived.





5.
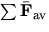Write the equation defining $\sum\mbox{$\bar{\bf F}$}_{\rm av}$.





6.
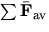Use the above equation to rewrite the equation of the principle of linear impulse and momentum in terms of $\sum\mbox{$\bar{\bf F}$}_{\rm av}$.





Angular Momentum

7.
Sketch Figure 8.14.












8.
Write the equation describing the principle of angular impulse and momentum for a rigid body.





9.
In the above equations I is the $\rule{0.8in}{.01in}$ $\rule{1.0in}{.01in}$ $\rule{0.4in}{.01in}$ $\rule{1.0in}{.01in}$ of the rigid body about its $\rule{1.0in}{.01in}$ $\rule{0.4in}{.01in}$ $\rule{1.0in}{.01in}$.

10.
The principle of angular impulse and momentum is the integral of a certain equation. Write this equation below.





11.
Suppose A and B are rigid bodies in two dimensional motion in the same plane, and suppose that they are subjected only to forces and couples they exert on each other, that is other forces and couples are $\rule{1.4in}{.01in}$. In this case, the total angular momentum is conserved, such that,

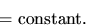
\begin{displaymath} ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~ = {\rm constant}.\end{displaymath}

12.
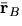What are $\mbox{$\bar{{\bf r}}$}_A$ and $\mbox{$\bar{{\bf r}}$}_B$ in the above equation?





13.
Is it possible that the total angular momentum is conserved if the external forces and couples are not zero. Explain your answer.






14.
Conservation of angular momentum       can       cannot       apply to an arbitrary number of rigid bodies. If it does apply, explain when it applies. (Circle the correct answer.)






Impacts

This section may not be covered in this class.


Chapter Summary

Read this section.