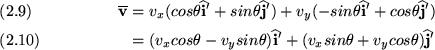EML 4930:Dynamic systems I
The dot product of two vectors is a scalar, so the dot product is sometimes
called the 'scalar product'. The dot product of two vectors ![]() and
and ![]() is denoted by
is denoted by ![]() (pronounced 'a dot b'). In dynamics the dot
product is used to define the work and power, to reduce a vector to
components, and to reduce vector equations to scalar equations.
(pronounced 'a dot b'). In dynamics the dot
product is used to define the work and power, to reduce a vector to
components, and to reduce vector equations to scalar equations.
Consider two vectors ![]() and
and ![]() with
an angle
with
an angle ![]() between them as shown in Figure 1.
between them as shown in Figure 1.
assume that the Cartesian coordinate representation of ![]() and
and ![]() given by
given by
| (1) |
| (2) |
Hence ![]()
Hence ![]()
Suppose a vector ![]() has Cartesian coordinate
representation
has Cartesian coordinate
representation
| (3) |

The cross product of two vectors ![]() and
and ![]() written as
written as ![]() and pronounced 'a cross b').Since the cross product of
and pronounced 'a cross b').Since the cross product of ![]() and
and ![]() is a vector, the cross product is
also called the vector product to distinguish it from the scalar
product ( the dot product). In dynamics the cross product is used to
define the moment
is a vector, the cross product is
also called the vector product to distinguish it from the scalar
product ( the dot product). In dynamics the cross product is used to
define the moment ![]() , and the angular momentum
, and the angular momentum ![]() Also the cross product is part of the formulas for velocity and
acceleration of points on spinning solids ( e.g.
Also the cross product is part of the formulas for velocity and
acceleration of points on spinning solids ( e.g. ![]()
Consider two vectors ![]() and
and ![]() with
an angle
with
an angle ![]() between them as shown in Figure 2. Again, assume that the
cartesian coordinate representation of
between them as shown in Figure 2. Again, assume that the
cartesian coordinate representation of ![]() and
and
![]() are given by
are given by
| (4) |
| (5) |
The cross product may be expressed as follows
| (6) |
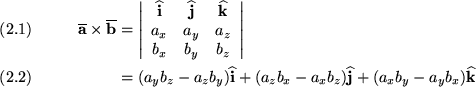
The following laws and special cases of the cross product are worth knowing
well. It is assumed that ![]() is a scalar.
is a scalar.
Hence ![]()
Hence
![]()
![]()
![]() (assuming a standard right handed coordinate system). See Figure 3 for
convenient memorizing these formulas.
(assuming a standard right handed coordinate system). See Figure 3 for
convenient memorizing these formulas.
The first distributive law above may be used ( in lieu of the determinant formula) to compute the cross products in terms of the cartesian components of the vectors. For example, suppose
| (7) |
| (8) |
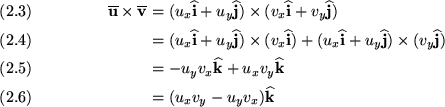
A vector ![]() in the (x,y) coordinate system with unit
vectors
in the (x,y) coordinate system with unit
vectors ![]() and
and ![]() is given by
is given by
| (9) |
To represent ![]() in the new coordinate system, one must
first express the unit vectors
in the new coordinate system, one must
first express the unit vectors ![]() and
and ![]() in terms of the unit vectors
in terms of the unit vectors ![]() and
and
![]() To do this consider the diagram shown in
Figure 5
To do this consider the diagram shown in
Figure 5
It is seen that
![]()
Using these expressions for ![]() and
and ![]() it follows that
it follows that