Fast Fourier Transform

When sound waves are viewed on an oscilloscope via microphone, there is a visual combination of waves with different frequencies. This will appear as a baseline wave with specific amplitude and higher frequency waves riding on top of it. In order to analyze the different frequency contributions in a particular wave, a different method of analysis must be implemented. The decomposition of a signal into a combination of sinusoids is known as a Fourier transform. This representation contains a summation of waves with different frequencies and amplitudes and is equivalent to the original function. In order for a computer to decompose a signal into its Fourier components, it has to take discrete data points and use an algorithm to determine the magnitude contribution of each frequency component of the signal. The process of obtaining the Discrete Fourier transform through use of algorithms is known as a Fast Fourier Transform (FFT). Once these components are analyzed, a plot of amplitude versus frequency is created to visualize the relative contributions of each frequency to the signal. An example of a Fourier transform is shown below. The major frequency of the low ‘A’ occurs at 220 Hz, but it also contains components at 440 Hz and 660 Hz, which are integer multiples of the fundamental frequency (Sequential values of n in the guitar analysis).

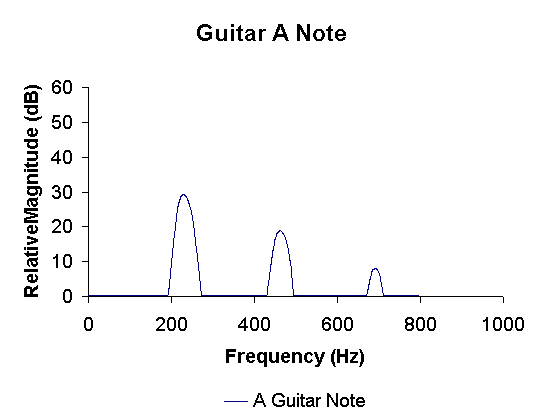
Figure 1: The FFT of a low 'A' played on guitar.

This fundamental frequency is the first mode of the note, which is the lowest frequency that produces a sinusoidal wave for a specific length of the guitar string. The other two modes are designated by the second and third frequency components, each having a lower magnitude contribution than the previous.