Guitar String Analysis

A guitar string can be modeled as a vibrating string fixed at its ends. The following steps detail the process and derivation of this model. Analyze the string by its differential element,

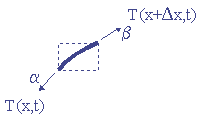
where the tension at each end of the element is different, the angles alpha and beta are not the same, and the horizontal tension is balanced so that the element is constrained to move only in the vertical direction. Using the above assumption, the sum of forces in the horizontal and vertical directions are as follows.

,

The variable ‘u’ is the vertical displacement as a function of one dimensional space and time. T is the tension in the string, and rho is the mass per unit length. Next the combinations of sine and cosine are combined to form the tangents of the two angles. The difference of the tangents is then written as the change in vertical to horizontal displacement ratio. The difference of these ratios can be used by taking the limit as delta x approaches zero to write the equation in differential form.

,

This differential equation can be solved using separation of variables where u is the product of a function of x and time. The solution has the following form,

,

,

The solution involves the sum of all the vibration modes and the coefficients weight the frequency contributions. The frequency is denoted by lambda and the wave speed depends on the tension and density.