Tuning

In order to play two of the same note and have them be in harmony, they must be tuned. The process of tuning can correct for phase and frequency difference between two waves. For ideal sound quality, two notes will have the same frequency and be in phase. The phase relationship between two waves describes the relative position of a peak of one wave to the corresponding peak of another wave. When these peaks coincide, the waves are said to be in phase, but when the peaks are not coincidental, the waves are said to be out of phase. In the phase analysis of wave summation, there are two distinct types of interference. The first is known as constructive interference.

Constructive interference occurs when the wave peaks coincide. This leads to increased amplitude of the combined wave relative to either single wave. In the other type, destructive interference, the wave peaks are exactly 180° out of phase and the waves will cancel each other out. Both of these phenomena are shown on the following plots.

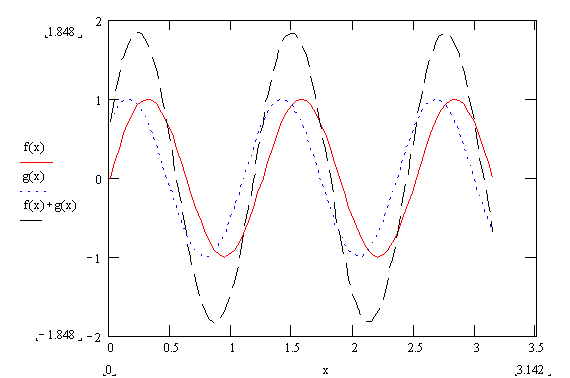
Figure 2: Summation of waves f(x) and g(x) when waves are nearly in phase.

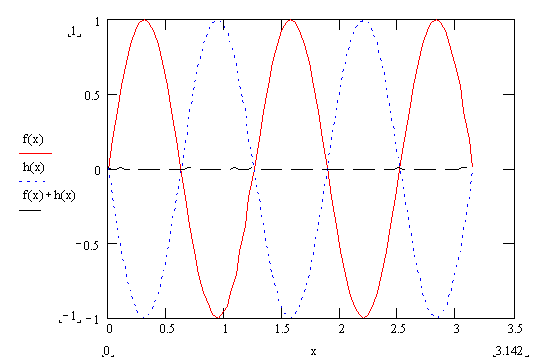
Figure 3: The summation of two waves f(x) and h(x) when the waves are totally out of phase.

Figure 2 shows that when the two waves are nearly in phase, the amplitude of the combined wave is much greater than the amplitude of either individual wave. Figure 3 shows that when 2 waves are completely out of phase, the resulting wave has zero amplitude.

An additional component of tuning two notes is the frequency relationship between the notes. As the frequency difference between the notes increases, they move closer to being two different notes with distinct pitches. As the frequency difference between the notes decreases, they will approach the same pitch and eventually begin to exhibit the phenomenon of beats. Beating is a result of the oscillating phase difference between two waves of nearly identical frequencies. As the waves begin to propagate, they will exhibit constructive interference because of the minute phase difference, but as the waves propagate further, the phase difference will begin to increase. This increase is due to the slight difference in frequency between the waves. As this difference in phase oscillates, there will be oscillating regions of constructive and destructive interference. The beat phenomenon is shown in the following plot where f1(t)=sin(t) and f2(t)=sin(1.1*t).

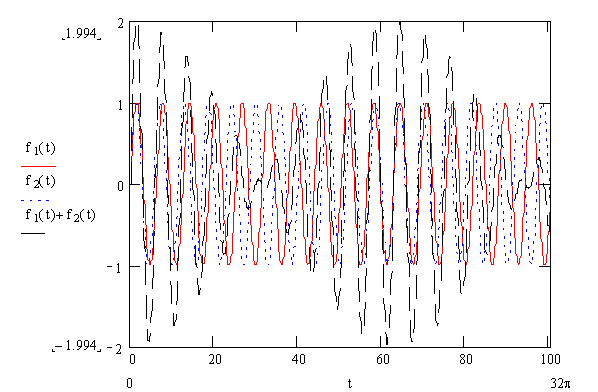
Figure 4: The summation of two waves with close frequencies exhibits the beat phenomenon.