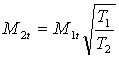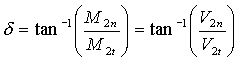Oblique Shock
|
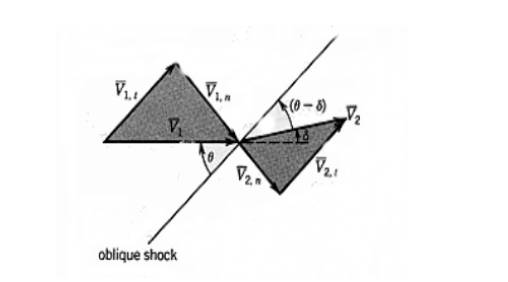
The following
diagram gives a geometrical representation of what an oblique shock wave
looks like when broken down into its velocity components. The interest lies with the fact that the
tangential component of velocity does not change. This is due to the fact that the tangential component of the
velocity stays parallel with the shock front. Therefore, the velocity does not change. |
||
|
|
|
|
|
|
V1 =
Inlet Velocity V2 = Exit
velocity after going through oblique shock line q =
shock wave angle d = diffuser
cone angle |
|
|
|
|
|
|
Because there is no change in tangential velocity,
relations between mach numbers, the shock wave angle (q), and the deflection angle (d) can be deduced. The governing equations
for oblique shock are: |
||
|
|
|
|
|
|
|
M = Mach# |
|
|
|
n denotes normal component |
|
|
|
t denotes tangential component |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
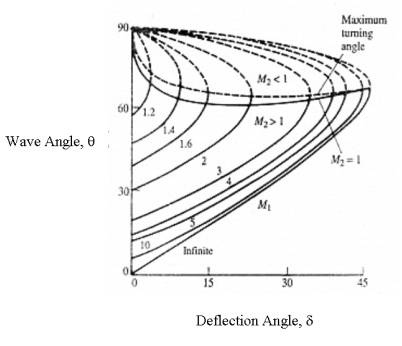
For the
ramjet inlet designer, q may not always be given. For this reason, trigonometric relations
between the right triangles formed above and properties
of normal shock yield the following table dependent only upon initial
Mach# and diffuser cone angle, d. |
||
|
|
|
|
|
|
|
|
|
|
|
|