Counterflow Experiment

Counterflow is a unique heat transfer mode of He II. Unlike classical convection, heat transfer in He II is via the relative motion of the two fluids: the normal fluid carries the entropy and heat away from the heat source, and a counterflowing superfluid serves to eliminate net mass flow. The velocity of the normal fluid u is related to the heat flux q by q=ρ s T u, where ρ is the He II density and s is the specific entropy [1]. This heat transfer mode is much more efficient than classical convection, and it leads to an effective thermal conductivity of He II much higher than any other materials [2]. He-II has therefore been widely utilized for cooling scientific and industrial equipment such as superconducting magnets, particle colliders, superconducting power transmission cables, RF accelerator cavities, and satellites [2].

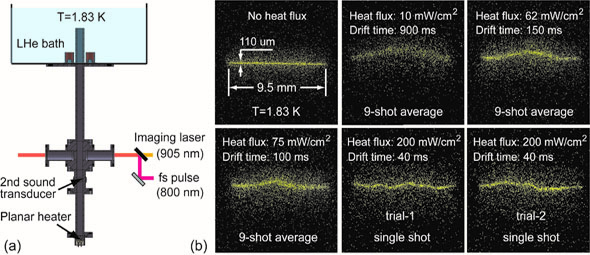
Figure 1: (a) Schematic diagram of the experimental setup; (b) Typical fluorescence images showing the motion of He₂^* tracer lines in thermal counterflow in He-II at 1.83 K. At heat fluxes above about 80 mW/cm², the tracer line distorts randomly, indicating turbulent flow in the normal fluid.

Pioneering studies by Vinen (our collaborator) showed that when the heat flux exceeds a small critical value, turbulence can appear spontaneously in the superfluid as a tangle of quantized vortices [3], which impairs the superior heat transfer capability of He II. Schwarz revealed in his seminal simulation work that this vortex tangle can be produced and maintained by the mutual friction [4-5]. This physical picture was examined in recent years by more sophisticated numerical simulations [6-7]. However, all these studies assumed a laminar flow in the normal fluid with a constant velocity field for simplicity. In our recent experiments, we applied the He₂ tracer line tracking technique to study thermal counterflow. We observe that at small heat fluxes, a straight tracer line deforms into a nearly parabolic, indicating a laminar Poiseuille velocity profile in the normal fluid. As the heat flux is further increased, the tail part of the tracer line becomes flattened. This flattening is very intriguing and is suspected to be caused by mutual friction between the normal fluid and the vortices that accumulate near the channel walls. At sufficiently high heat fluxes, a straight tracer line deforms randomly, suggesting turbulent flows (see Fig.1). These observations provide the first concrete experimental evidence that the normal fluid can become turbulent in counterflow [8-9]. Our statistical study has also revealed surprising non-classical scaling behaviors of the normal fluid turbulence which have stimulated various related researches in many other groups.

The normal-fluid turbulence in counterflow can result in strong heat-flux fluctuations that inevitably affect the performance of the cooling systems. Yet, our existing knowledge of turbulence obtained from classical fluids is not applicable to the normal-fluid turbulence in counterflow. This is because in the normal fluid the dissipation from the mutual friction occurs at all scales since the two fluids move oppositely. This situation is in marked contrast to classical turbulence where the energy dissipation is important only below a small scale called Kolmogorov scale [10]. Understanding the novel normal-fluid turbulence and its influence on the vortex-tangle dynamics is now regarded as one of the most challenging problems in quantum fluid research. A systematic characterization of the normal fluid turbulence will be indispensable for developing such an understanding. This characterization, which is currently conducted in our lab, will potentially benefit the design of He II based cooling systems.

Reference:

[1]  D.R. Tilley and J. Tilley, Superfluidity and superconductivity. (A. Hilger; Published in association with the University of Sussex Press, Boston, 1986), 2nd ed.
[2]  S.W. Van Sciver, "Helium Cryogenics", in International Cryogenics Monograph Series (Springer US, Boston, MA, 2012).
[3]  W.F. Vinen, "Mutual Friction in a Heat Current in Liquid Helium II. I. Experiments on Steady Heat Currents", Proc R Soc Lon Ser A 240, 114-127 (1957).
[4]  K.W. Schwarz, "Theory of Turbulence in Superfluid He-4", Phys Rev Lett 38 (10), 551-554 (1977).
[5]  K.W. Schwarz, "Turbulence in Superfluid-Helium - Steady Homogeneous Counterflow", Phys Rev B 18 (1), 245-262 (1978).
[6]  M. Tsubota, M. Kobayashi, and H. Takeuchi, "Quantum hydrodynamics", Phys Rep 522 (3), 191-238 (2013).
[7]  H. Adachi, S. Fujiyama, and M. Tsubota, "Steady-state counterflow quantum turbulence: Simulation of vortex filaments using the full Biot-Savart law", Phys Rev B 81 (10) (2010).
[8]  W. Guo, D.P. Lathrop, M.L. Mantia, and S.W. Van Sciver, "Visualization of two-fluid flows of superfluid helium-4 at finite temperatures", Proc Natl Acad Sci USA 111, 4653 (2014).
[9]  A. Marakov, J. Gao, W. Guo, S.W. Van Sciver, G.G. Ihas, D.N. McKinsey, and W.F. Vinen, "Visualization of the normal-fluid turbulence in counterflowing superfluid He-4", Phys Rev B 91 (9) (2015).
[10] P.A. Davidson, Turbulence : an introduction for scientists and engineers. (Oxford University Press, Oxford, UK ; New York, 2004).