18.2.1.1 Solution stanexl-a

Question:

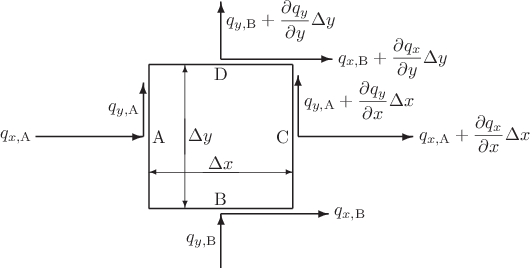
Derive the Laplace equation for steady heat conduction in a two-dimensional plate of constant thickness $\delta$ . Do so by considering a little Cartesian rectangle of dimensions ${\Delta}x\times{\Delta}y$ . A sketch is shown below:

$\begin{figure}\begin{center} \leavevmode \setlength{\unitlength}{1pt} \begin{pi... ...ac{\partial q_y}{\partial y} \Delta y$}} } \end{picture}\end{center}\end{figure}$

Assume Fourier’s law:

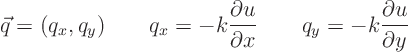
$\begin{displaymath} \vec q = (q_x,q_y) \qquad q_x = - k \frac{\partial u}{\partial x} \qquad q_y = - k \frac{\partial u}{\partial y} \end{displaymath}$

Here

is the temperature, assumed independent of

. Also,

is the heat conduction coefficient of the material. The vector $\vec{q}$ is the heat flux density. Vector $\vec q$ is in the direction of the heat flow. Its magnitude $\vert\vec{q}\vert$ equals the heat flowing per unit area normal to the direction of flow.

If you want the heat flow $\dot Q$ through an area element ${\rm d}{S}$ that is not normal to the direction of heat flow, the expression is

$\begin{displaymath} \dot Q = \vec q \cdot{\vec n}{ \rm d}s \end{displaymath}$

Here ${\vec n}$ is the unit vector normal to the surface element ${\rm d}{S}$ . Positive $\dot{Q}$ means a heat flow through the surface element in the same direction as ${\vec n}$ .

Assume that no heat is added to the little rectangle from external sources.

Answer:

If the temperature distribution is steady, then the net heat flowing into the rectangle must be zero. If the net heat flow in was positive, the rectangle would heat up. So it would not be steady. The same way, if the net heat flow in was negative, so net heat coming out, the rectangle would cool down and not be steady.

So what you need to do is find the expression for the net heat flowing into the little rectangle.

To get this net heat flow, you need to sum the contributions of all the four segments of the perimeter. It is here accurate enough to assume that the heat flux on each side can be approximated by the heat flux at the center point of the segment, point A, B, C, or D. It is also accurate enough to ignore the variations of the derivatives of the heat fluxes over the rectangle.

Note also that heat flow along the boundary does not move heat in or out.

Next plug in Fourier’s law as given. Divide by the volume ${\Delta}x{\Delta}y\delta$ of the rectangular piece and take the limit that the dimensions go to zero. That then produces the Laplace equation.

You should be able to find arguments like the above in many books on engineering mathematics.