18.2.1.2 Solution stanexl-b

Question:

Derive the Laplace equation for steady heat conduction using vector analysis. Assume Fourier’s law as given in the previous question. In vector form

$$\vec q = - k \nabla u$$

Assume that no heat is added to the solid from external sources.

Answer:

Consider an arbitrary volume $V$ of the solid. The net heat flow out of the volume $V$ per unit time is given by

$$Q_{\rm net out} = \int_S \vec q \cdot\vec n { \rm d}S$$

where $S$ is the outside surface of the volume and $\vec n$ the unit vector normal to the surface element ${\rm d}{S}$.

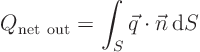
This heat flux must be zero. If there was net heat flow in or out, the volume would heat up, respectively cool down.

Now use the Gauss-Ostrogradski theorem to convert the surface integral to a volume integral. Then note that if an integrand always integrates to zero, regardless of which volume is integrated over, then that integrand must be zero.

Show that this means that

$$\nabla\cdot\vec q = {\rm div} \vec q = 0$$

Plug in Fourier’s law, and there you have the Laplace equation, assuming that $k$ is constant. (If it is not, you get an equation given in earlier examples.)