20.4 Using the boundary or initial condition

After you have found the general solution of the partial differential equation as described in the previous sections, you probably want to find the remaining undetermined function that it involves by applying a given boundary or initial condition. To do so:

1. Write the boundary condition in terms of a single parameter, call it $s$.
2. Plug the general solution to the partial differential equation into it.
3. Call the argument of the unknown function, say $\alpha$, and express everything else in terms of $\alpha$ instead of $s$ by solving for $s$ in terms of $\alpha$.
4. That will produce the expression for the unknown function for any value of its argument. Plug that back into the general solution which is now fully determined.

Example

Question: (5.30 continued) Solve

$$y u_x + x u_y = cu$$

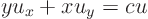
with initial condition

$$u=x^2+y \qquad \mbox{on} \qquad x + y = 1,$$

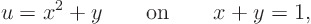
Solution:

The general solution to the partial differential equation for this example is given by

$$u(x,y) = C_2(y^2 - x^2) (x+y)^c.$$

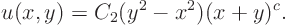
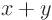
Plug that into the initial condition on the line $x+y$ $\vphantom0\raisebox{1.5pt}{$=$}$ 1 in order to figure out what function $C_2$ must be:

$$C_2(y^2 - x^2) (x+y)^c = x^2+y \qquad \mbox{on} \qquad x + y = 1,$$

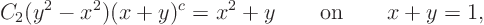
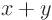
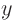
Don’t try to deduce one-parameter function $C_2$ directly from an expression involving two different parameters. Instead convert to a single parameter by expressing one parameter in terms of the other. In this case, you can use $x+y$ $\vphantom0\raisebox{1.5pt}{$=$}$ 1 to express $y$ in terms of $x$ as $y$ $\vphantom0\raisebox{1.5pt}{$=$}$ $1-x$. That gives

$$C_2(1 - 2x + x^2 - x^2) (x+1 - x)^c = x^2+ 1 -x \qquad \mbox{on} \qquad y = 1 - x,$$

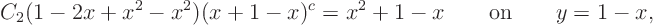
or cleaned up

$$C_2(1 - 2x) = x^2 -x + 1$$

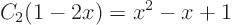
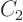
Now you have an expression for function $C_2$ in terms of a single parameter. To get the function itself, give some name to its parameter that is not already used. Call the argument, say, $\alpha$. So $C_2$ $\vphantom0\raisebox{1.5pt}{$=$}$ $C_2(\alpha)$. According to the initial condition above

$$\alpha \equiv 1 - 2x.$$

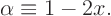
Solve this for $x$ in terms of $\alpha$,

$$x = {\textstyle\frac{1}{2}}(1-\alpha)$$

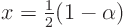
and plug that into the expression for $C_2$ to get an expression for function $C_2(\alpha)$ in terms of $\alpha$ only:

$$C_2(\alpha) = \Big({\textstyle\frac{1}{2}}(1-\alpha)\Big)^2 -{\textstyle\frac{1}{2}}(1-\alpha) + 1$$

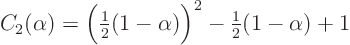
or worked out

$$C_2(\alpha) = {\textstyle\frac{1}{4}}\alpha^2 + {\textstyle\frac{3}{4}}.$$

Figure 20.3: Region where $u$ is determined by an initial condition given on the line $x+y=1$.

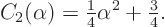
Now that function $C_2$ has been identified, plug it into the general solution, valid everywhere,

$$u(x,y) = C_2(y^2 - x^2) (x+y)^c.$$

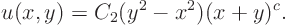
to get the final solution

$$u(x,y) = \Big({\textstyle\frac{1}{4}}(y^2 - x^2)^2 +{\textstyle\frac{3}{4}}\Big) (x+y)^c.$$

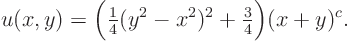
Note that this solution is only valid in the grey region of figure 20.3; the characteristics in the white region never intersect the line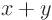 $x+y$ $\vphantom0\raisebox{1.5pt}{$=$}$ 1. To find the solution there, you would need an initial condition on, say, the line $x+y$ $\vphantom0\raisebox{1.5pt}{$=$}$ $-1$.

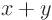
You see how important it is to graph the characteristics.