| Analysis in Mechanical Engineering |
|
© Leon van Dommelen |
|
20.6 First order equations in more dimensions
The procedures of the previous subsections extend in a logical way to
more dimensions. If the independent variables are
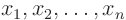 , the first order quasi-linear partial
differential equation takes the form
, the first order quasi-linear partial
differential equation takes the form
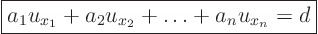 |
(20.6) |
where the 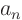 and
and 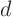 may depend on
may depend on 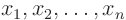 and
and  .
.
The characteristic equations can now be found from the ratios
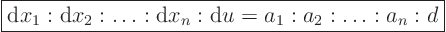 |
(20.7) |
After solving 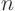 different ordinary differential equations from this
set, the integration constant of one of them, call it
different ordinary differential equations from this
set, the integration constant of one of them, call it 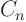 can be
taken to be a general
can be
taken to be a general 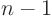 -parameter function of the others,
-parameter function of the others,
and then substituting for  from the other
ordinary differential equation, an expression for
from the other
ordinary differential equation, an expression for  results
involving one still undetermined,
results
involving one still undetermined, 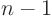 parameter function
parameter function 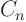 .
.
To find this remaining undetermined function, plug in whatever initial
condition is given, renotate the parameters of 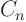 to
to
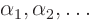 and express everything in terms of them to
find function
and express everything in terms of them to
find function 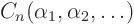 .
.
![]() , the first order quasi-linear partial
differential equation takes the form
, the first order quasi-linear partial
differential equation takes the form
![]() to
to
![]() and express everything in terms of them to
find function
and express everything in terms of them to
find function ![]() .
.