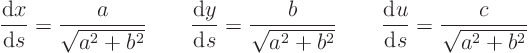| Analysis in Mechanical Engineering |
|
© Leon van Dommelen |
|
20.2 Numerical solution
It is certainly straightforward to numerically solve the two ordinary
differential equations of the previous subsection along a
characteristic line using say a Runge-Kutta method. You would need to
start from some point at which an initial or boundary condition is
given.
If you find the solution along each of a densely spaced set of
characteristic lines, you have essentially found  everywhere.
everywhere.
Of course, if 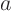 is zero somewhere in the region of interest, it may
be a better idea to find
is zero somewhere in the region of interest, it may
be a better idea to find  and
and 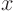 as functions of
as functions of 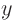 instead of
instead of
 and
and 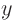 as functions of
as functions of 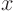 , by taking suitable ratios from
(20.4). Or you could just find all three variables as
function of the arc length
, by taking suitable ratios from
(20.4). Or you could just find all three variables as
function of the arc length 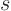 along the characteristic lines, by
solving
along the characteristic lines, by
solving
This allows either 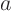 or
or 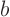 to be zero; it only fails if both are
zero at the same point, and that is a true physical problem rather
than a mathematical one.
to be zero; it only fails if both are
zero at the same point, and that is a true physical problem rather
than a mathematical one.
![]() everywhere.
everywhere.
![]() is zero somewhere in the region of interest, it may
be a better idea to find
is zero somewhere in the region of interest, it may
be a better idea to find ![]() and
and ![]() as functions of
as functions of ![]() instead of
instead of
![]() and
and ![]() as functions of
as functions of ![]() , by taking suitable ratios from
(20.4). Or you could just find all three variables as
function of the arc length
, by taking suitable ratios from
(20.4). Or you could just find all three variables as
function of the arc length ![]() along the characteristic lines, by
solving
along the characteristic lines, by
solving