In hand computations with integer matrices in homework or an
exam in this class, the objective is to avoid fractions in the
algebra. So you try to select a pivot which is 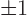 .
.
Note that there may not be such a pivot. In that case, you may be
still be able to avoid fractions by partial pivoting. Or else you
might be able to avoid them by multiplying the row being replaced by
an integer greater than 1 instead of 1.
If that works, it should normally be done. However, if
you want to identify matrices 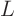 and
and 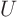 in the
in the 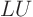 theorem, you
can only multiply the row being replaced by 1. Otherwise the
theorem does not work. So you may have to live with fractions.
theorem, you
can only multiply the row being replaced by 1. Otherwise the
theorem does not work. So you may have to live with fractions.
![]() and
and ![]() in the
in the ![]() theorem, you
can only multiply the row being replaced by 1. Otherwise the
theorem does not work. So you may have to live with fractions.
theorem, you
can only multiply the row being replaced by 1. Otherwise the
theorem does not work. So you may have to live with fractions.