| Analysis in Mechanical Engineering |
|
© Leon van Dommelen |
|
13.1 Finding inverses using GE
Note: if you are required to find an inverse using minors in this
class, do not use any GE, even for attractive simplifications.
Note: If a matrix is orthonormal, its inverse must be found
using a transpose in this class.
Finding the inverse of a matrix is usually a bad idea. But if you do
need it, you may use the following trick:
-
1.
- Create an augmented matrix in which the
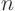 right hand side
column vectors are the columns of the unit matrix.
right hand side
column vectors are the columns of the unit matrix.
-
2.
- Reduce the matrix to row canonical form using Gaussian
elimination as described earlier. In other words
-
3.
- For a nonsingular matrix
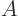 ,
, 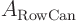 will be a unit
matrix and
will be a unit
matrix and 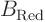 will be the desired
will be the desired 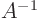 . (For a
singular matrix, one of the pivots will be found to be zero in the
reduction to echelon form, and there is no inverse matrix.)
. (For a
singular matrix, one of the pivots will be found to be zero in the
reduction to echelon form, and there is no inverse matrix.)
Note that what you are really doing in the above is solving the system
of equations 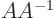

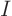 for the columns of
for the columns of 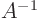 . The
only trick is that if you reduce the matrix all the way to a unit
matrix, the solution
. The
only trick is that if you reduce the matrix all the way to a unit
matrix, the solution 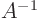 becomes the same as the right hand side
of the reduced system.
becomes the same as the right hand side
of the reduced system.
Also note that the most efficient way to find the inverse, in terms of
operations, is still LU decomposition. Normally this would take
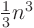 operations to find
operations to find 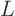 and
and 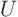 and then
and then 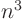 operations
to find the
operations
to find the 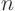 columns of
columns of 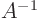 . But the right hand sides to the
. But the right hand sides to the
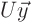

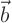 systems are unit vectors, which are mostly zeros. If
you use this to avoid computing coefficients in
systems are unit vectors, which are mostly zeros. If
you use this to avoid computing coefficients in 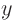 that are
automatically zero, you can reduce the operations by
that are
automatically zero, you can reduce the operations by 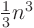 .
.
![]()
![]()
![]() for the columns of
for the columns of ![]() . The
only trick is that if you reduce the matrix all the way to a unit
matrix, the solution
. The
only trick is that if you reduce the matrix all the way to a unit
matrix, the solution ![]() becomes the same as the right hand side
of the reduced system.
becomes the same as the right hand side
of the reduced system.
![]() operations to find
operations to find ![]() and
and ![]() and then
and then ![]() operations
to find the
operations
to find the ![]() columns of
columns of ![]() . But the right hand sides to the
. But the right hand sides to the
![]()
![]()
![]() systems are unit vectors, which are mostly zeros. If
you use this to avoid computing coefficients in
systems are unit vectors, which are mostly zeros. If
you use this to avoid computing coefficients in ![]() that are
automatically zero, you can reduce the operations by
that are
automatically zero, you can reduce the operations by ![]() .
.