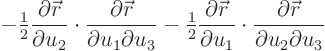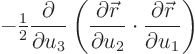| Analysis in Mechanical Engineering |
|
© Leon van Dommelen |
|
D.1 Orthogonal coordinate derivatives
Since there is no fundamental difference between the three orthogonal
coordinates, it suffices to show that
The other derivatives with 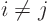 go the same way, and the
derivatives with
go the same way, and the
derivatives with 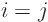 can then be evaluated by writing
can then be evaluated by writing 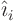 as a
cross product of the other two unit vectors.
as a
cross product of the other two unit vectors.
Now to derive the above result, the only thing we know a priori is
that the derivative of a unit vector is normal to the unit vector, so:
But it is not obvious why 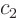 would have to be
would have to be
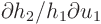 and
and 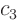 would have to be zero.
would have to be zero.
Recall however that 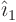 was defined as
was defined as
and if we differentiate this with respect to 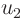 , one of the terms
will involve the desired derivative of
, one of the terms
will involve the desired derivative of 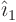 :
:
Since we can change the order of differentiation without changing the
derivative, we must have
so, writing out the derivative
Now compare 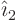 components in both sides, noting that the
derivative of
components in both sides, noting that the
derivative of 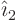 is normal to
is normal to 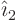 . Then you see that the
value of
. Then you see that the
value of 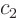 given above is indeed correct.
given above is indeed correct.
But it is not clear from the above why 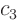 would have to be zero.
To find that out, we dot the derivative
would have to be zero.
To find that out, we dot the derivative
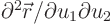 with
with
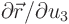 , because the latter derivative is by
definition
, because the latter derivative is by
definition 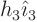 , so the dot product will give
, so the dot product will give
So to show that 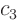 is zero, we must show that the dot product above
is zero. That can be done with a bit of manipulation. The only thing
you can do, of course, is shuffle the derivatives around. In
particular, if you pull the derivative with respect to
is zero, we must show that the dot product above
is zero. That can be done with a bit of manipulation. The only thing
you can do, of course, is shuffle the derivatives around. In
particular, if you pull the derivative with respect to 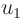 to the
front of the entire thing,
to the
front of the entire thing,
where the final term corrects for the additional term generated by
pulling the 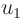 derivative out. Note now that the dot product in
the parentheses above is zero since the vectors are orthogonal. Only
the final term survives.
derivative out. Note now that the dot product in
the parentheses above is zero since the vectors are orthogonal. Only
the final term survives.
Next, ask yourself: why pull the 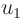 derivative out? Why not
derivative out? Why not 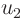 ?
After all,
?
After all, 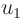 and
and 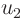 appear completely symmetrically in the
expression. That suggests that really, what we should do is pull
appear completely symmetrically in the
expression. That suggests that really, what we should do is pull
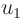 out of half the term and
out of half the term and 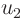 out of the other half. That
gives
out of the other half. That
gives
That is seen to be the same as
and the dot product in parenthesis is zero. So indeed 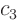 is zero.
is zero.
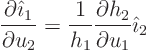
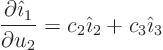
![]() was defined as
was defined as
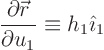
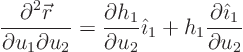
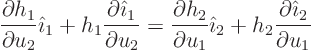
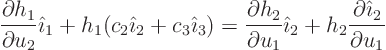
![]() would have to be zero.
To find that out, we dot the derivative
would have to be zero.
To find that out, we dot the derivative
![]() with
with
![]() , because the latter derivative is by
definition
, because the latter derivative is by
definition ![]() , so the dot product will give
, so the dot product will give
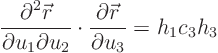
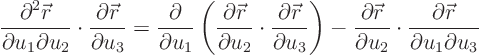
![]() derivative out? Why not
derivative out? Why not ![]() ?
After all,
?
After all, ![]() and
and ![]() appear completely symmetrically in the
expression. That suggests that really, what we should do is pull
appear completely symmetrically in the
expression. That suggests that really, what we should do is pull
![]() out of half the term and
out of half the term and ![]() out of the other half. That
gives
out of the other half. That
gives