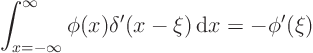| Analysis in Mechanical Engineering |
|
© Leon van Dommelen |
|
A.1 Distributions
A delta function is not a function in the normal sense. Infinity is
not a proper number.
However, delta functions have a property that can be used to
define them. That property is called the “filtering property.” If you multiply a delta function by a
smooth function 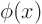 and integrate over all
and integrate over all 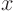 , you get the value
of the function at the location of the delta function:
, you get the value
of the function at the location of the delta function:
The reason is that the delta function is everywhere zero except at the
single point 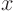

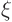 . So you can replace
. So you can replace 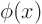 by
by 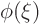 without changing anything. And
without changing anything. And 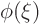 is a constant that can be
taken out of the integral.
is a constant that can be
taken out of the integral.
You can reverse that statement and define the delta function as the
distribution
that produces the result above for any
smooth function 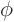 . (The functions
. (The functions 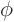 are normally further
constrained by a requirement that they must become zero at their
ends.)
are normally further
constrained by a requirement that they must become zero at their
ends.)
In a similar way you can also define the derivative of the delta
function, the dipole 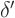 . It is the distribution for which,
for any smooth
. It is the distribution for which,
for any smooth 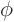 ,
,
To see why you want to define it this way, perform a formal integration
by parts.
![]() and integrate over all
and integrate over all ![]() , you get the value
of the function at the location of the delta function:
, you get the value
of the function at the location of the delta function:
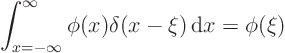
![]() . (The functions
. (The functions ![]() are normally further
constrained by a requirement that they must become zero at their
ends.)
are normally further
constrained by a requirement that they must become zero at their
ends.)
![]() . It is the distribution for which,
for any smooth
. It is the distribution for which,
for any smooth ![]() ,
,