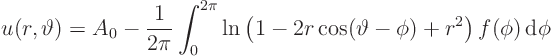| Analysis in Mechanical Engineering |
|
© Leon van Dommelen |
|
22.5 Finding the Green's function
The previous section found the solution to the ideal flow in
a circle in the form
We can write it directly in terms of the given 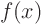 if we substitute
in the expressions for the Fourier coefficients:
if we substitute
in the expressions for the Fourier coefficients:
We can clean it up by combining terms and interchanging integration
and summation:
This we can clean up even more by giving a name to the function within
the curly brackets:
Nice, not?
We can even simplify 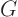 by converting to complex exponentials
and differentiating:
by converting to complex exponentials
and differentiating:
The last equation applies because the sums are geometric series.
Integrating and cleaning up produces
So, we finally have the following Poisson-type integral expression
giving  directly in terms of the given
directly in terms of the given 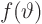 , with no
sums:
, with no
sums:
Neat!
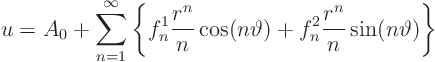
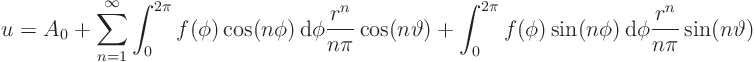
![\begin{displaymath}
u = A_0 + \int_0^{2\pi}
\sum_{n=1}^\infty
\left\{
\f...
...n(n\phi) \sin(n\vartheta)]
\right\}
f(\phi) { \rm d}\phi
\end{displaymath}](img1609.gif)
![\begin{displaymath}
u = A_0 + \int_0^{2\pi}
\left\{\sum_{n=1}^\infty \frac{r^n}{n\pi}\cos(n[\vartheta-\phi])\right\}
f(\phi) { \rm d}\phi
\end{displaymath}](img1610.gif)
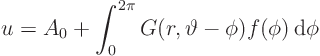
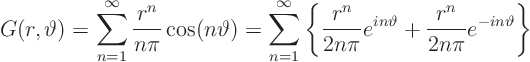
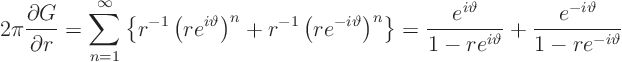
![]() directly in terms of the given
directly in terms of the given ![]() , with no
sums:
, with no
sums: